MATHEMATICAL, PHYSICAL AND CHEMICAL SCIENCES
UNDERLYING SANTILLI'S INTERMEDIATE NUCLEAR
SYNTHESES, WITHOUT RADIATIONS
Full scientific presentation available in the monograph
I. Gandzha and J Kadeisvili,
New Sciences for a New Era:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli, Sankata Printing Press, Nepal (2011),
http://www.santilli-foundation.org/docs/RMS.pdf
EXPERIMENTAL VERIFICATIONS IN CLASSICAL PHYSICS, PARTICLE PHYSICS, NUCLEAR PHYSICS, CHEMISTRY, SUPERCONDUCTIVITY, ASTROPHYSICS, ANTIMATTER AND COSMOLOGY
5.1 INTRODUCTION
5.1A. The unreassuring conditions of 20th century particle physics
5.1B. Mutation of particles in interior conditions
5.1C. Mutation of spacetime caused by physical media
5.2. EXPERIMENTAL VERIFICATIONS IN PARTICLE PHYSICS
5.2A. Experimental verification of the mutation of magnetic moments.
5.2B. Experimental verification with the meanlives of unstable hadrons
5.2C. Experimental verifications with arbitrary local causal speeds
5.2D. Experimental verification via the Bose-Einstein correlation
5.2E. Characterization of hadronic media
5.3. EXPERIMENTAL VERIFICATIONS IN NUCLEAR PHYSICS.
5.3A. The unreassuring condition of 20th century nuclear physics.
5.3B. Experimental verification with nuclear magnetic moments.
5.3C. Experimental verifications with the nuclear force
5.4. EXPERIMENTAL VERIFICATIONS IN CHEMISTRY AND SUPERCONDUCTIVITY
5.4A. Experimental verifications in chemistry
5.4B. The unreassuring condition of 20th century superconductivity
5.4C. Animalu's isosuperconductivity
5.4D. Experimental verification of Animalu's isosuperconductivity
5.4E. Initial basic laws of hadronic mechanics
5.5. EXPERIMENTAL VERIFICATION WITH THE BEHAVIOR OF LIGHT
5.5A. The inevitability of the ether as a universal medium
5.5B. Experimental verification with light propagating in water.
5.5C. Santilli isoredshift
5.5D. Experimental confirmation of Santilli isoredshift
5.5E. Experimental verification with the colors our atmosphere
5.6. EXPERIMENTAL VERIFICATIONS IN ASTROPHYSICS
5.6A. The unreassuring condition of 20th century astrophysics and cosmology.
5.6B. Absence of universe expansion
5.6C. Absence of "dark matter"
5.6D. Absence of "dark energy"
5.6E. Experimental verification with quasar redshifts
5.7. EXPERIMENTAL VERIFICATION WITH ANTIMATTER AND COSMOLOGY
5.7A. The unreassuring condition of 20th century antimatter and cosmology
5.7B. Experimental verification of Santilli's isodual theory of antimatter
5.7C. Santilli's iso-, geno-, and hyper-cosmologies.
Appendix 5.7A: Newton-Santilli universal gravitation
CHAPTER 5:
EXPERIMENTAL VERIFICATIONS IN PARTICLE PHYSICS, NUCLEAR PHYSICS, CHEMISTRY, SUPERCONDUCTIVITY, ASTROPHYSICS, ANTIMATTER AND COSMOLOGY
5.1 INTRODUCTION
5.1A. The unreassuring conditions of 20th century particle physics
Despite historical successes for the structure of the hydrogen atom and other systems, the first half of the 20th century saw numerous authoritative voices of doubt on the final character of of special relativity and quantum mechanics, such as: Heisenberg's studies on covering nonlinear theories; Dirac's support for a new theory without divergencies; and others.
During the remaining half of the 20th century, these authoritative voices of doubt were ignored, other sound dissident views were "disqualified" via the abuse of academic authority without technical counter-arguments and, as Santilli puts it, special relativity and quantum mechanics were assumed as being exactly valid for all conceivable conditions existing in the universe, expectedly until the end of time..
This occurrence created an unreassuring condition because all physical theories are known by experts to have limitations. Particularly unreassuring has been the protracted claim of the exact validity of special relativity and quantum mechanics in scattering experiments because of numerous insufficiencies denounced by Animalu and Santilli in their recent memoir
Nonunitary-isounitary scattering theory, I: Basic Formulation without divergencies for low energy reversible scattering
A. O. E. Animalu and R. M. Santilli, to appear,
Contributed paper to the 2008 IARD CONFERENCE, Thessaloniki, Greece, submitted for publication,
Among said limitations, we recall the manifest irreversibility over time of high energy scatterings compared to the well known reversibility of the very mathematical structure, axioms and physical laws of special relativity and quantum mechanics; the necessary point-like character of all particles under quantum descriptions for which all possible scatterings among charged particles are essentially of Coulomb nature (except for possible decays); and other reasons.
Therefore, the unreassuring condition of the 20th century physics is of such a serious character to cast shadows on the very validity of a number of "experimental results" that, when dealing with relativistic quantum treatments of deep mutual penetration of particles, are called by Santilli "experimental beliefs."
To stimulate a collegial return to serious scientific values in physics, at his recent invited (and paid) plenary talk at the inauguration ceremony of the new Research Institute for Hypercomplex Systems in Geometry and Physics in Moscow, Russia, on May 4-5, 2009 (see the Talk power point), Santilli suggested the conduction of systematic collegial studies on the identification of the following:
I) CONDITIONS OF EXACT VALIDITY OF SPECIAL RELATIVITY AND QUANTUM MECHANICS, They are assumed by Santilli as being those of the original conception of the theory by Einstein, Minkowski, Heisenberg, Schroedinger, Dirac and other founders, and are given by point-like particles and electromagnetic waves propagating in vacuum conceived as empty space. Hence, special relativity and quantum mechanics are assumed as being exactly valid for the structure of the hydrogen atom, particles in accelerators, and numerous other systems in which the mutual distance of particles is sufficiently big to allow their effective point-like approximation. In this case, we have the sole presence of action-at-a-distance, potential interactions and the systems are entirely represented with the sole knowledge of the Hamiltonian, as well known.
II) CONDITIONS OF APPROXIMATE VALIDITY OF SPECIAL RELATIVITY AND QUANTUM MECHANICS. They are assumed by Santilli as being conditions causing the partial or total mutual penetration of the wavepackets and/or charge distribution of particles, as typically the case for mutual distances of the order of 10-13 cm = 1 fm, under which we have additional contact interactions that are not representable with a Hamiltonian (variationally nonselfadjoint interactions). In this case, the representation of systems require a second operator besides the Hamiltonian, whose only known invariant selection is given by Santilli isounit.
The 20th century physics managed to claim the exact validity of special relativity and quantum mechanics under the latter conditions too via the introduction of completely arbitrary parameters and functions of unknown physical origin, their fit from the experimental data, and then the claim of the exact validity of preferred theories. Santilli has shown that these arbitrary parameters are, in reality, a direct measurement of the deviations of special relativity and quantum mechanics from the conditions considered, with truly paradoxical cases, such as that of the Bose-Einstein correlation reviewed below, whose fit of the experimental data requires the double of the maximal number of parameters admitted by quantum axioms.
III) CONDITIONS OF INAPPLICABILITY OF SPECIAL RELATIVITY AND QUANTUM MECHANICS. They are given by conditions under which the theories permit no quantitative treatment at all despite the throwing into the equations of all desired arbitrary parameters and functions, as it is the case for the synthesis of the neutron as occurring in stars studied in the next chapter, classical studies of antimatter, mechanics compatible with thermodynamical laws, and others. In this case, Santilli insists that special relativity and quantum mechanics are merely "inapplicable" and cannot be considered as being "violated" because not conceived for the conditions considered.
The most undeniable experimental verifications of hadronic mechanics and its underlying iso-, geno- and hyper relativities are those of Class III studied in detail in the following chapters. The applications industrially most important are those dealing with energy releasing processes, that are in fact strictly irreversible, and they are treated in Chapter 7. Note that the latter require Santilli Lie-admissible genomechanics we cannot possibly review to avoid a prohibitive length. Serious scholars are referred to Santilli's latest and most comprehensive memoir in the field
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
For a collection of historical papers in irreversibility, we also refer the serious scholar to the volume
"Irreversibility and Nonpotentiality in Statistical Mechanics"
A. Schober, Editor,
Hadronic Press (1984)
whose reading should be done by keeping in mind the crucial Theorem 1.1 on the impossibility of eliminating nonpotential irreversible interactions via the reduction of macroscopic systems to elementary constituents, thus identifying the roots of Santilli Lie-admissible genomechanics at the most ultimate level of nature. A technical knowledge of these aspects is important for the serious scholar to dismiss political claims voiced for personal gains, such as the claim that "irreversibility disappears at the level of elementary particles," a statement disproved by Theorem 1.1.
Again, to prevent an excessive length, in this chapter we shall present a few experimental verifications of Santilli isorelativity and hadronic mechanics restricted to its isotopic branch for conditions of Class II only to show the merely approximate character of special relativity and quantum mechanics compared to the exact validity of the covering isotheories. For a comprehensive and detailed study of the experimental verifications of hadronic mechanics, we refer the serious scholar to the following monograph from which this chapter has been derived
Hadronic Mathematics, Mechanics and Chemistry, Volumes IV and V,
R. M. Santilli, International Academic Press (2008)
5.1B. Mutation of particles in interior conditions
Recall that the intrinsic characteristic of particles, such as mass, charge, spin, magnetic moment, meanlife, etc., parity, are not altered by interactions permitted by special relativity and quantum mechanics. This occurrence originates from the sole admission of action-at-a-distance potential interactions with corresponding definition of particles as irreducible unitary representations of the Galilei symmetry at the nonrelativistic level, and of the Lorentz-Poincare' symmetry at the relativistic level.
The covering isorelativity and hadronic mechanics characterize the broader notion of isoparticles, namely, as irreducible isounitary isorepresentations of the Galilei-Santilli isosymmetry at the nonrelativistic level, and of the Lorentz-Poincare'-Santilli isosymmetry at the relativistic level. In turn, the transition from the conventional symmetries for the vacuum to the covering isosymmetries implies that ordinary particles generally experience an alteration of all their characteristics, including intrinsic characteristics, Santilli calls mutation, in the transition from motion in vacuum at large mutual distances to conditions of mutual penetration. Such a mutation originates from the addition of contact, zero-range nonpotential interactions represented with Santilli isounits under which all characteristics are generally changed, e.g., because of the change of their units.
Santilli's notion of mutation is used in the literature on hadronic mechanics in order to distinguish it from the so-called "deformations" because the latter verify the Theorems of Catastrophic Inconsistencies of Noncanonical and Nonunitary Theories studied in Section 3.8. The reader should recall that Santilli's mutations bypass these theorems because they reconstruct canonicity or unitarity on isospaces over isofields, while deformations are afflicted by catastrophic inconsistencies because because of their definition on conventional spaces over conventional fields. In short, the only known invariant representation of nonpotential interactions is that via the isounits, as a result of which the mutation of particle is unavoidable.
It should be noted that the notion of mutation is also referred to in the literature on hadronic mechanics as isorenormalization. In this case, "renormalization" is referred to conventional renormalizations for strictly Lagrangian or Hamiltonian theories, while "isorenormalizations" is referred to their image under isotopic lifting in which case Santilli mutations are unavoidable as shown in this and in the following chapters. As Santilli puts it:
It is generally believed that an electron immersed in the core of a star undergoing gravitational collapse has the same intrinsic characteristics as those nicely observed in our laboratories under sole action-at-a-distance interactions. Besides having no experimental confirmation, such a theological belief has no credibility, not even minimal or remote, since the conditions here referred to imply the acceptance of the perpetual motion within physical media since the electron has to maintain the exact rotational and other conventional symmetries.
The notion of mutation was first introduced by Santilli in 1967 at the algebraic level as part of his Ph. D. thesis via the transition from a Lie algebra to a Santilli Lie-admissible algebra
Embedding of Lie-algebras in nonassociative structures
R. M. Santilli, Nuovo Cimento Vol. 51, 570-576 (1967).
then re-examined in 1978 via the addition of the mutation from Lie algebras to Lie-Santilli isoalgebras,
On a possible Lie-admissible covering of Galilei's relativity
in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
R. M. Santilli, Hadronic J. Vol. 1, 223-423 (1978)
and finally presented at the particle level also in 1978 via the original proposal to build hadronic mechanics,
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
in which mutated electrons (ordinary electron immersed within hyperdense hadronic medium) were called "eletons," although the name of "isoelectrons" subsequently became of general use also because the prefix "iso" is applicable to all particles.
A technical knowledge of the notion of nonrelativistic isoparticles requires first a reading of the introductory paper (written by Santilli when visiting the ICTP in Trieste, in 1991 under the last invitation issued by Abdus Salam prior to his death)
The notion of nonrelativistic isoparticle
R. M. Santilli,
ICTP preprint # IC/91/265 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
and then a serious study of Santilli's isotopies of the Galilei relativity and symmetry available in the two volumes
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
R. M. Santilli,
Hadronic Press (1991)
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
R. M. Santilli,
Hadronic Press (1991)
A serious knowledge of the notion of relativistic isoparticle requires a study of Santilli's isotopies of special relativity and the Lorentz-Poincare' symmetry whose best presentation remains that of the following two volumes of 1995 (originally written when Santilli was visiting the JINR in Dubna, Russia, during the period 1992-1995)
"Elements of Hadronic Mechanics", Vol. I: "Mathematical Foundations"
R. M. Santilli
Ukraine Academy of Sciences (1995)
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
R. M. Santilli,
Ukraine Academy of Sciences (1995)
A serious knowledge of the covering notion of Lie-admissible genoparticle for irreversible conditions requires the additional study of the following two volumes (written when Santilli was a member of the Department of Mathematics of Harvard University under DOE support, although the first volume carries his affiliation at the Lyman Laboratory of Physics of Harvard University)
"Lie-Admissible Approach to the Hadronic Structure, I: Non applicability of the Galilei and Einstein Relativities,"
R. M. Santilli,
Hadronic Press (1978)
"Lie-Admissible Approach to the Hadronic Structure, II: Coverings of the Galilei and Einstein Relativities"
R. M. Santilli,
Hadronic Press (1982)
5.1C. Mutation of spacetime caused by physical media
The fundamental hypothesis underlying Santilli isorelativity and hadronic mechanics is that physical media, whether characterized by matter or light, alter the very structure of the Minkowskian spacetime of the vacuum. The applicability of isorelativity then follows from the direct universality of the Minkowski-Santilli isospacetime for all possible line elements with signature (+, +, +, -), and its related fundamental Lorentz-Poincare'-Santilli isosymmetry. The unique applicability of hadronic mechanics follows from unambiguous maps to operator formulations.
The first and most compelling experimental evidence on the mutation of spacetime is that studied in the next section on the local variation of the speed of light within physical media. In fact, it is easy to prove that no variation of the speed of light is possible without an alteration of spacetime itself called by Santilli a spacetime mutation.
It should be recalled that the reconstruction of a universal symmetry for a mutated spacetime requires an alteration of the very "units" of both, space and time. The mutation of space units is necessary to reconstruct, e.g., the rotational symmetry for all possible deformations of the sphere, while the mutation of the unit of time is necessary, e.g., to represent the deviations from the conventional time dilation for an electromagnetic wave propagating within a physical medium (see Section 3.10).
For the case of particles, we have a similar situation. An isolated electron in vacuum, being dimensionless, can be safely assumed to evolve according to our own time with unit I = 1 sec. However, when the same electron is immersed within a hyperdense medium, such as in the core of a star or in the interior of a proton as needed for the neutron synthesis, the same electron evolves according to an intrinsic time different than our own whose isounit can be numerically identified from experimental data, as we shall see.
Note that the "price to pay" for the insistence in maintaining our units of space and time under interior conditions is the breaking of basic spacetime symmetries since, as established by the Lie-Santilli isotheory, the latter are reconstructed as exact at the isotopic level only under isounits that are numerically the inverse of the alteration of conventional spacetime (Section 3.10).
Alternatively the assumption of the conventional spacetime within physical media implies that an electron in the core of a collapsing start is identical to an isolated electron in vacuum, a clearly unplausible expectation because the electron has a wavepacket that must be deformed when immersed within a hyperdense medium. It should be noted that the above mutations have a fundamental role in predicting basically new clean energies (see Chapter 7) that are unthinkable for special relativity and quantum mechanics precisely in view of their unverified assumption of their exact character within physical media.
The best and most technical presentation on the mutation of spacetime remains that available in Santilli's 1995 monographs Elements of Hadronic Mechanics quoted in the preceding section. For a recent comprehensive presentation one may study the five volumes
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V,
R. M. Santilli, International Academic Press (2008)
5.2. EXPERIMENTAL VERIFICATIONS IN CLASSICAL AND PARTICLE PHYSICS
5.2A. Experimental verification of the mutation of magnetic moments.
Classical verification
The most visible and convincing experimental verification of the mutation of the intrinsic characteristics of elementary and composite particles is the lack of existence in nature of perfect rigidity, implying the necessary deformability of the shape of a charged and spinning particle that, in turn, causes the necessary alteration of the intrinsic magnetic moment as established at the classical level. When one mutation is established, the mutation, in general, of spin, rest energy, charge, meanlife, parity, and other intrinsic characteristics follows via simple compatibility arguments, or via the use of the Lorentz-Poincare'-Santilli isotransforms.
Santilli's mutation of particles is rendered inevitable by the following evidence. In view of its very mathematical structure and axioms, quantum mechanics can solely represent particles as dimensionless points, in which case no mutation is conceptually or technically possible. By comparison, hadronic mechanics characterizes particles as extended, in which case mutations are unavoidable due to the lack of perfect rigidity in nature.
We can say that the notion of mutation did not exist in 20th century mainstream physics because nonrelativistic and relativistic quantum mechanics and their underlying spacetime symmetries are irreconcilably incompatible with deformations occurring in the physical reality. By comparison, deformations are readily represented by hadronic mechanics thanks to Santilli's isorotational symmetry that was build precisely for that scope while reconstructing the exact rotational symmetry on isospaces over isofields (Section 3.10).
In closing, we should remember that the classical counterpart of hadronic mechanics, known as the Hamilton-Santilli iso-, geno- and hyper-mechanics, have been proved to be "directly universal" in classical physics, that is, representing all possible discrete classical systems (universality) in the coordinate of the experimenter (direct universality), thus having incontrovertible experimental verifications in classical physics. As a matter of fact, serious experts in hadronic mechanics know that these classical verifications are the very foundation of the new operator theory.
Additionally, it should be recalled that said new mechanics are the only known capable of representing non-Hamiltonian systems with an action principle, as well as representing said systems in their actual shape, dimension and density. As a matter of fact, the representation via a variational principle is the very foundation for the operator treatment of nonpotential forces. As an illustration, the irreversible Hamilton-Santilli genomechanics is the only known mechanics characterizing via the optimal control theory the shape of the wing of an airplane under the resistive force caused by motion in our atmosphere. Following such a so novel a verification impossible with conventional mathematics and mechanics, there seems no point in providing additional verifications in classical physics.
Rauch's interferometric experiment on the neutron spinorial symmetry
The first direct experimental measurement of the deformability of the intrinsic magnetic moments of neutrons was announced by H. Rauch
H. Rauch et al., Hadronic J. Vol. 4
, 1280 (1981)
during Third Workshop on Lie-Admissible Formulations held at Harvard University in 1981, see the Proceedings
H. C. Myung and R. M. Santilli, Editor, Proceedings of the Third Workshop on
Lie-Admissible Formulations, Part A, Hadronic J. Vol. 4, issue no. 2, pp. 183-607 (l981).
H. C. Myung and R. M. Santilli, Editor, Proceedings of the Third Workshop on
Lie-Admissible Formulations, Part B, Hadronic J. Vol. 4, issue no. 3, pp. 608-1165 (l981).
H. C. Myung and R. M. Santilli, Editor, Proceedings of the Third Workshop on
Lie-Admissible Formulations, Part C, Hadronic J. Vol. 4, issue no. 4, pp. 1166-1625
(l981).
The measurements were conducted via a potentially historical neutron interferometric test of the 4π-spinorial symmetry of neutrons as presented in various papers of the time, such as
H. Rauch et al., Phys. Lett. A Vol 54, p. 425 (1975).
G. Badurek et al., Phys. Rev. D Vol. 14, p. 1177 (1976).
H. Rauch et al., Z. Physik B Vol. 29, p. 281 (1978).
H. Kaiser et al., Z. Physik A Vol. 291, p. 231 (1979).
Various calculations for a thermal neutron beam exposed to the intense fields in the vicinity of heavy nuclei, as it is the case for Rauch's experiment (see below) were done by G. Eder at the same 1981 meeting
G.Eder, Hadronic J. Vol. 4, p. 312 (1981) and Vol. 5, p. 750 (1982).
Eder's conclusion is that strong nuclear forces do not imply an appreciable effect due to the very small sectional area of their influence, while nuclear electric and magnetic fields do imply a measurable effect of the order of 1%, that is precisely the amount indicated by Rauch and his collaborators.
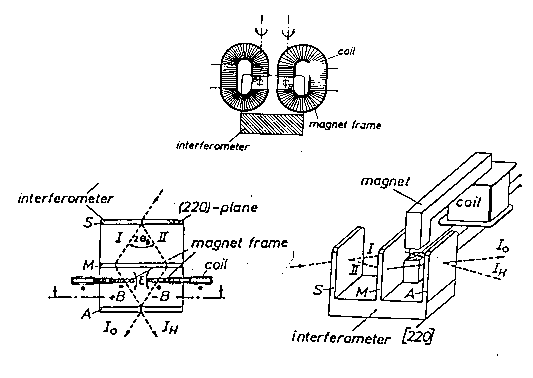
Figure 5.1: A view of Rauch's neutron interferometric experiment on the mutation of the intrinsic magnetic moment of neutrons under very intense external electric and magnetic nuclear fields.
In the experiment, a thermal neutron beam is first coherently split by a perfect crystal and then passes through the gap of an electromagnet in one (or both) branches. The beam is then coherently recombined by the perfect crystal as shown in Figure 5.1. The experimenters calibrated the field of the electromagnet to the value 7,496 G to achieve exactly two spin flips, i.e., a rotation of 4π = 720o, as predicted by the exact SU(2)-spin symmetry for the conventional value of the neutron magnetic moment in vacuum
When the neutron beam travels in empty space (namely the electromagnet gap is empty), the experimenters confirmed the exact occurrence of the 4π symmetry, thus providing a beautiful verification of quantum mechanics in the conditions under which it is applicable, that is, when neutrons can be all well approximated as massive points.
However, in order to avoid stray fields at the gap borders, the experimenters filled up the electromagnet gap with Mu-metal sheets. This essentially provided a test of the spinorial symmetry of neutrons under the intense electric and magnetic fields in the vicinity of Mu metal nuclei.
In all tests, Rauch and his collaborators did not
The above measurements do not contain the exact angle 720o, thus providing the first known experimental evidence of the breaking of the SU(2)-spin symmetry in particle physics.
Needless to say, the experiment is not final and must be repeated until the deviation is at least three times the error. By remembering that measurements (5.2) date back to 1978 (see later on for comments), these improvements can be done nowadays in a variety of ways, such as conducting the tests for a large multiple of 4π that would be resolutory, provided that the experimenters fill up the electromagnet gap with Mu-metal sheets or other heavy element (in which absence the tests would have no relevance for the test of mutation due to the weakness of nuclear fields).
Despite this unsettled aspect, Rauch measurements (5.2) are plausible indeed. In fact, they are confirmed by various deviation from quantum mechanical values of total nuclear magnetic moments (see Section 5.3), not to mention numerous theoretical works. Also, as recalled earlier, perfectly rigid bodies do not exist in the physical reality. Therefore, the amount of mutation for given external nuclear fields is certainly open to experimental resolutions, but its existence is beyond credible doubt since its denial implies the belief of perfect rigidity.
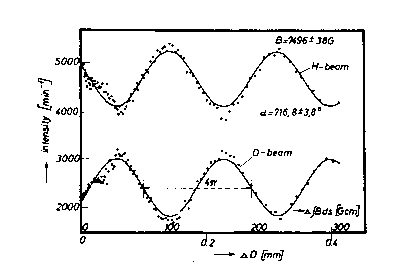
Figure 5.2: The plot of experimental data on the coherent recombination of the split neutron beams in Rauch's 4π neutron interferometric experiments of Figure 5.1. Note the loss of the sinusoidal character of the plot that, alone, establishes a deviation from the exact SU(2)-spin symmetry.
Also, the possible recovering of the full 720o angle is not sufficient to claim full confirmation of quantum mechanics in the conditions herein considered because there are several other aspects that have to be obtained. One of them is the sinusoidal character of the curve on the coherent recombination of the two split neutron beams. The experimental data shown in Figure 5.2 establish a clear loss of such a sinusoidal character in an amount that is indeed a multiple of the error. On strict scientific grounds, this is sufficient, alone, to provide experimental evidence of mutation of the intrinsic magnetic moment of neutrons.
It should be indicated that, to our been knowledge, Rauch's experiment has never been duplicated since its conduction in the mid 1970s along the lines reported above. More specifically, numerous neutron interferometric experiments have been evidently conducted since that time, but all of them either with the neutron beam moving in vacuum or under a splitting of the beam into opposite contributions yielding no mutation of the neutron magnetic moment. The authors would appreciate any indication of actual neutron interferometric experiments conceived and realized in such as a way to maximize (rather than minimize or avoid) the exposure of the neutron beam to intense nuclear fields without any splitting into opposing contributions or other manipulations.
Santilli's representation of Rauch's interferometric measurements
The first quantitative representation of Rauch's measurements (5.2) was reached by Santilli at the Third Workshop on Lie-admissible Formulations, of 1981, in the memoir
Experimental, theoretical and mathematical elements for a
possible Lie-admissible generalization of the notion of particle under
strong interactions, The Institute for Basic Research
Contributed paper to the l980 Clausthal Conference on Differential
Geometric Methods in Mathematical Physics,
Hadronic J. Vol. 4, 1166-1257 (l981)
then re-elaborated in the following 1989 paper
Operator Isospecial Relativities for Interior Problems in
Particle Physics,
The Institute for Basic Research,
Hadronic J. Suppl.Vol. 4B, issue no. 3 (l989)
Santilli reviewed his representation of Rauch's experiment during his visit of the ICTP in Trieste, Italy, of 1991,
Theory of mutation of elementary particles and its application to Rauch's experiment on the spinorial symmetry
R. M. Santilli,
ICTP preprint # IC/91/46 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
The study was then finalized in 1993 when Santilli was visiting the Joint Institute for Nuclear Research, Dubna, Russia,
Communication of the JINR no. E4-93-352, 1993
with subsequent printed version that is adopted in this section
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons,
R. M. Santilli,
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
A recent comprehensive treatment is available in Santilli's monograph
Hadronic Mathematics, Mechanics and Chemistry, Volume IV,
R. M. Santilli, International Academic Press (2008)
Rauch's experiment deals with the SU(2)-spin symmetry of the neutron when propagating within a physical medium characterized by very intense fields. Since the neutron has spin 1/2, the representation of the data requires the Dirac-Santilli isoequation outlined in Section 3.11Q whose technical knowledge is assumed to prevent venturing vacuous pseudo-judgments.
When the gap of the electromagnet is empty of matter (here assumed to be the vacuum), the neutrons cannot experience any mutation (see the l.h.s of Figure 5.3), and the predictions of quantum mechanics are exact.
However, when the gap of the electromagnet is filled up with dense Mu-metal sheets, neutrons experience a deformation of their charge distribution that, in turn, implies a necessary alteration of their intrinsic magnetic moment, as requested by the electrodynamics of charged, spinning and deformed spheres. Note in this case that the mutation of the intrinsic magnetic moment occurs without mutating the spin 1/2 of the neutron, evidently in view of the long range character of the acting forces.
The fact that the measured angle is consistently smaller than that expected ("angle slow down effect") implies that the intrinsic magnetic moment of the neutron is decreased in the considered conditions.
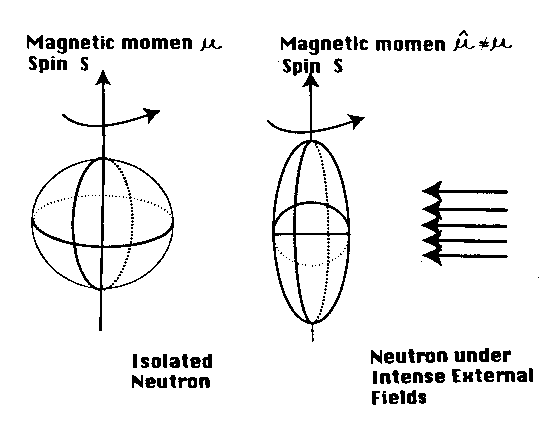
Figure 5.3: The elementary physical interpretation of Rauch's measurements of Figures 5.1 and 5.2 via a deformation of the charge distribution of neutron of the order of 1%. Note that the deformation must be such as to provide an oblate spheroidal ellipsoid as a condition to represent the "angle slow down effect," since only such oblate deformation implies a decrease of the intrinsic magnetic moment. Note also that the spin 1/2 of the neutron is not mutated in Rauch's experiment due to the external long range nature of the electric and magnetic fields acting on the neutron and the absence of contact interactions. The preservation of the spin 1/2 implies that quantitative treatments can be obtained via nonunitary transforms of conventional relativistic treatments, technically expressed by the fact that the irreducible representation of the Lorentz-Poincare'-Santilli isosymmetry are regular (the "exceptional representations" implying an alteration of the spin that cannot be obtained via such a simple map).
The achievement of a numerical, exact and invariant representation of experimental data (5.2) via relativistic hadronic mechanics is also elementary. Since the neutron is a spinning particle, it is natural to assume that the only possible mutation is that of the charge distribution of the neutron from its spherical shape (necessary for quantum mechanics) to a spheroidal ellipsoid with semiaxes
The ellipsoid will then be a prolate or oblate depending, respectively, on whether
Rauch measured a deviation from the SU(2)-spin transformation in the angle α of the spin precession along the third axis. Such a transformation is best represented via Dirac's equation according to the well known law
where the γs are the conventional Dirac gamma matrices.
The use of Dirac-Santilli isoequations and related isotopic SU(2)-spin symmetry of Section 3.11Q then implies the applicability of the following isolaw
By using the Minkowski-Santilli isometric expressed via the b-characteristic quantity, and the explicit form of the Dirac-Santilli isogamma matrices, Santilli obtains the expression
where the exact value of 4π for the isoangle α* should be expected by experts in isotopies. In fact, all isotopies reconstruct as exact on isospace over isofields conventionally broken symmetries. In this case, the reconstruction of the exact SU(2)-spin symmetry requires that the isoangle be equal to the exact value 4π. In this case, the deviation occurs only in the projection of the isotheory in our conventional spacetime, exactly as realized in Eq. (5.7).
The above expression immediately provides the first numerical values of the b-characteristic quantities
Next, the mutation here considered cannot possibly change the density of the hyperdense medium inside the neutron, namely, the mutation must be volume preserving. By assuming that the original sphere has a radius normalized to one, this condition implies that
from which we obtain the numerical value of third characteristic quantity
namely, relativistic hadronic mechanics characterizes an oblate spheroidal deformation, with a consequential decrease of the intrinsic magnetic moment, precisely as needed to represent the experimental data.
To achieve a numerical value of the mutated intrinsic magnetic moment
m* Santilli assume that in first approximation
But, the Dirac-Santilli isoequation of Section 3.11Q implies the following ration between mutated and conventional magnetic moments
Santilli reaches in this way the numerical value
namely, the density of the thermal neutron beam is insufficient to affect the maximal causal speed, that remains the speed in vacuum (Isoaxiom I). The numerical value of the mutated intrinsic magnetic moment is then given, in average, by
namely, the mutation of the intrinsic magnetic moment in Rauch's experiment is confirmed by the Dirac-Santilli isoequations as being of the order of 1 %,.
This completes the Santilli's numerical, exact and invariant representation of Rauch's experimental data on the 4π neutron interferometric experiment via relativistic hadronic mechanics, representation that is manifestly impossible for quantum mechanics.
In summary, relativistic hadronic mechanics permits a direct, numerical, exact and invariant representation of:
1) The actual, extended, nonspherical and deformable charge distributions of neutrons and their density via the basic isounit
where b1-2, b2-2, b3-2 represent the semiaxes of the spheroidal ellipsoid and b4-2 geometrizes the density of the medium in the interior of the neutron here having the value 1 from the preservation of the speed of light in vacuum within the Mu-metal sheets;
2) All possible deformations of these shapes via a dependence of the isounit, e.g., on the intensity of the external electric and magnetic fields originating from the nuclei of the Mu-metal nuclei;
3) The "angle slow-down effect", namely, the systematic decrease of the angle of precession due to a decrease of the intrinsic magnetic moment for the physical conditions considered;
4) The necessarily oblate mutation/deformation of the charge distribution of the neutron to represent said angle slow down effect;
5) All the above exact numerical representations are obtained by reconstructing the exact SU(2)-spin symmetry on isospaces over isofield, while the same symmetry remains broken in conventional treatments.
In closing, the authors feels a duty to recall rather extreme political interferences by the academic establishment against the finalization of Rauch's fundamental experiment, in documented knowledge of its paramount importance for the prediction and treatment of new clean energies so much needed by mankind (Chapter 9). In fact, Rauch's measurements reported in this section date back to 1978. Following their presentation at the above quoted meeting of 1981, Rauch and his associates were prohibited to continue the measurements at their original laboratory in Grenoble, France, under the conditions herein considered (with the electromagnet gap filled up with heavy metals).
The unreassuring character of the 20th century physics is fully identified by the fact that, despite the passing of some 30 years, this fundamental aspects of scientific knowledge (the exact or broken character of the SU(2)-spin symmetry under external nuclear fields) remains fundamentally unsolved. In fact, all repetitions of Rauch's experiment occurred since 1978 known to the authors were carefully conceived and conducted such to have the thermal neutron beam move in vacuum, the expected deviation in one branch compensated by that of the other branch, or different settings under which the verification of quantum mechanics is unquestionable (the authors would appreciate the indication of true experimental resolutions not quoted here).
Due to the societal implications of the case, Santilli felt obliged to report the organized obstructions against the experimental resolution of the issue in the 1984 book
Ethical Probe of Einstein's Followers in the USA: An Insider's View
R. M. Santilli, Alpha Publishing (1984)
and in the related 1,315 pages of documentation dated 1985
Documentation of the Ethical Probe, Voplume I
Documentation of the Ethical Probe, Volume II
Documentation of the Ethical Probe, Volume III
R. M. Santilli, Alpha Publishing (1985)
In view of the above, Santilli's deep conviction is that, without a control of scientific ethics in mainstream physics, no truly basic advance for the much needed new clean energies can be effectively achieved due to obstructions, discreditations and other disruptive actions by organized interests on pre-established doctrines under abused academic credibility.
5.2B. Experimental verification with the meanlives of unstable hadrons
A direct experimental verification of the validity of Santilli isorelativity and its underlying isogeometry and Lorentz-Poincare'-Santilli isosymmetry (Sections 3.10 and 3.11) in the interior of hadrons is provided by the anomalous behavior of the meanlife of unstable hadrons with speed. In fact, according to current experimental data reviewed below, such a behavior:
1) is at variance with the behavior predicted by special relativity,
where c is the speed of light in vacuum;
2) confirms the behavior predicted by Santilli isorelativity, Isoaxiom III, Eq. (3.95),
3) constitutes an indirect verification of the iso-Doppler law, Isoaxiom IV, Eq. (3.98).
Recall that the center-of-mass behavior of a particle in an accelerator must obey the laws of special relativity (because the particle moves in vacuum under external electromagnetic interactions). Yet, nonlocal interactions are known to imply deviations from special relativity laws. The issue is therefore how nonlocal effects in the interior of hadrons can manifest themselves in their exterior behavior in a particle accelerator.
Blokhintsev and his school at the JINR in Dubna pioneered in paper
D. I. Blokhintsev, Phys. Lett.{\bf 12}, 272 (1964)
the hypothesis that such nonlocal internal effects can manifest themselves via departures from the Minkowskian behavior of the meanlife of unstable particles with speed, while the center-of-mass trajectory follows Einsteinian theories exactly, and submitted certain generalized time-dilation laws. The problem was subsequently studied by several authors, such as
D. Y. Kim, Hadronic J. {\bf 1}, 1343 (1978)
H. B. Nielsen and I. Picek, Nucl. Phys. B {\bf 211}, 269 (1983)
and others. This resulted in a variety of generalized time dilation laws. In the 1983 papers
Lie-isotopic lifting of special relativity
for extended deformable particles
Lie-isotopic lifting of unitary symmetries and
of Wigner's theorem for extended deformable particles,
Santilli submitted his isotopies of the special relativity with underlying isotopies of the Minkowskian spacetimes and the Lorentz-Poincare' symmetry as a form of geometrization of the physical medium in the interior of hadrons with isotopic law (5.23). The latter law was subsequently proved by Aringazin
as being "directly universal," i.e., including all possible generalizations of the time dilation law via different expansions in terms of different parameters and with different truncations ("universality") in the fixed reference frame of the experimenter ("direct universality").
A recent comprehensive treatment is available in Santilli's monograph
Hadronic Mathematics, Mechanics and Chemistry, Volume IV,
The covering character of Santilli isorelativity now acquires its full experimental significance. Prior to the unified isotopic laws, experimenters had to test a considerable variety of different time dilation laws without having any mean for a possible selection due to unavoidable approximations. With Santilli universal isolaws these problems are eliminated and the tests can be restricted to the unifying law (5.18).
Preceding generalized time dilation laws left basically unsolved the problem of their compatibility with the Einsteinian center-of-mass behavior, thus remaining unsettled even in the event of final experimental verifications. By comparison, the Lorentz-Poincare'-Santilli isosymmetry has been constructed for the purpose of yielding conventional center-of-mass trajectories, a feature achieved by preserving all ten Poincare' generators and related conserved quantities and isotopically lifting instead their Lie algebra into the Lie-Santilli isoproduct
The first phenomenological verification of the iso-Minkowskian geometry for the interior of hadrons has been provided by Nielsen and Picek
H. B. Nielsen and I. Picek, Nucl. Phys. B {\bf 211}, 269 (1983)
who computed deviations from the Minkowskian geometry inside pions and kaons via standard gauge models in the Higgs sector. These phenomenological studies resulted in a "deformed Minkowski metric" inside pions and kaons of the type
The first direct experimental verification of the anomalous behavior of the meanlives of unstable hadrons with speed was reached by Aronson et al.
S. H. Aronson et al., Phys. Rev. D Vol. 28, 495 (1983)
who measured a clear anomalous behavior of the meanlife of the Ko in the energy range 30-100 GeV. Subsequent experiments conducted by Grossman et al.
N. Grossman et al., Phys. Rev. Lett. Vol. 59, 18 (1987)
claimed a confirmation the Einsteinian behavior of the meanlife of the particle considered.
Nevertheless, Grossman's experiment is afflicted by equivocal theoretical and phenomenological assumptions reviewed below, to such an extent to raise doubt as to whether Grossman's experiment was specifically intended to recover conventional laws (as it has been the case for all neutron interferometric tests following that by Rauch outlined in the preceding section and virtually all experimental data departing from Einsteinian theories).
To begin the appraisal of Grossman's experiment, one should never forget that special relativity is clearly inapplicable within media of low density such as air or water due to insufficiencies beyond credible doubt (Section 3.10). Therefore, the belief without protracted and repeated tests that special relativity is exactly valid in the hyperdense media inside hadrons has no serious credibility, thus casting doubts on excessive theoretical and phenomenological assumptions in the elaboration of raw experimental data by Grossman's team.
Next, deviations from the Einsteinian behavior inside mesons had been previously shown by Nielsen and Picek. Additionally, Grossman's experiment was done for the energy range 100-350 GeV that is different than the range 30-100 GeV of Aronson's experiment. Consequently, Grossman's test cannot be claimed as confirming the validity of Einsteinian laws within hadrons on any, even minimally credible scientific ground.
Furthermore, an exact fit of Aronson's anomalous measurements between 30 and 100 GeV was done by Cardone et al.
On a possible energy-dependence of the Ko/s lifetime,
by reaching the numerical values (see Figure 5.5 for the plot)
On a possible energy-dependence of the Ko/s lifetime,
Cardone et al (loc. cit.) also achieved an exact fit via Santilli's isolaw (5.18) of the two seemingly discordant measurements by Aronson and Grossman for the energy range from 30 to 400 GeV for the interior of the Ko-particle, resulting in the following experimental values for the characteristic b-quantities for Ko
Values (5.33)-(5.37) also confirm the prediction of Santilli isorelativity in the range 30-400 GeV according to which the b4 quantity (being a geometrization of the density of a given hadron) is constant for the particle considered (although varying from hadron to hadron), while the dependence in the velocity rests with the space bk-quantities.
Note Santilli's reconstruction of the exact Lorentz and Poincare' symmetries at the isotopic level for all anomalous time behavior of meanlives, as proved by Cardone et al (loc. cit.). By contrast, the quantity α of Eq. (2.3) was called by Nielsen and Picek (loc. cit.) the Lorentz asymmetry parameter. In reality the Lorentz symmetry is exactly valid for the deformed metrics when reconstructed with respect to Santilli's isounit
Finally, the behavior of the meanlives of unstable hadrons with speed was re-examined
by Arestov et al.
Experimental evidence on the iso-Minkowskian character
of the hadronic structure,
who focused the attention first on the energy range selection rule
that can be applied to re-elaborate the initial data on
decays. By taking into account the results
as they were done, Arestov et al. performed Monte Carlo simulations
of the main features of Grossman's experiment via the use of the same statistics, and reached conclusions dramatically different than those by Grossman et al.
Aronson et al. also provided attention to the parameters used by Grossman in the formula dN/dt for the proper time
evolution. The strong correlation of said parameters causes a generally regular dependence
of the parameters on entities not present in the formula, such
as a
number of run offs, etc., apart from the systematic uncertainties.
Therefore, the above dependence
shadows Grossman's weak energy dependence that is dominant in this case,
as can be seen from the latter large values of the correlation elements.
Additionally, Grossman solved the problem of non-correlated fit
by selecting the kaon momenta greater than 100 GeV/c. By means of that
energy cut off, Grossman obtained the data sample in which the CP violating terms
contribute up to 1.6 %. However, it is unrealistic to look for the deviations from the Minkowskian decay law of the order of 1.6 %.
More realistic is to test the decay law for the kaons for deviations of the order of 10-3 percent,
as suggested in the fits by Cardone et al (loc. cit.).
In fact, the assumption of 1.6 % contribution from PC violation
in Grossman's data elaboration implies looking for a large energy dependence of their tau function, thus rendering it meaningless to look
for more realistic deviations.
The large inefficiency (error) of Grossman's tests occurred because they had not
been optimized for the problem at hand. Basically, the experimental design and
data selection rules were those of conventional relativistic studies in weak interactions. This implies that Grossman et al (loc. cit.) assumed special relativity in the data elaboration as shown in Figure 5.6. Their "experimental results" are, therefore, crucially dependent on the assumed theory.
R. M. Santilli,
Lettere Nuovo Cimento Vol. 37, 545-555 (1983)
R. M. Santilli,
Lettere Nuovo Cimento Vol. 38, 509-521 (1983)
R. M. Santilli, International Academic Press (2008)
where T is fixed integrodifferential (nonlocal) operator for the hadron considered. In this way, the Lorentz-Poincare'-Santilli isosymmetry admits generalized internal laws due to the new interactions represented by the isotopic element T. Therefore, the use of the Lorentz-Poincare'-Santilli isosymmetry assures the compliance of particles with the Einsteinian center-of-mass behavior in particle accelerators, in a way fully compatible with nonlocal internal effects. Note that this is a fundamental point for the historical legacy on the nonlocality of the strong interactions.
where α is a constant with numerical values different for different mesons, thus confirming the dependance of the deviations from special relativity on the density of the hadron considered. It is evident that the above generalized metric is a particular case of Santilli isometric (3.3.57) with numerical values in terms of the characteristic quantities b = 1/n from the data provided by Nielsen and Picek
Note the change in numerical value of the characteristic quantity b4 in the transition from pions to kaons, which change is necessary for Santilli isorelativity. In fact, all hadrons have approximately the same size, but different rest energies, thus having different densities. Consequently treatments of different hadrons via Santilli isorelativity requires different characteristic quantities b4.
F. Cardone, R. Mignani and R. M. Santilli,
J. Phys. G: Part. Phys. vol. 18, L61-L65 (1992)
In the subsequent paper
F. Cardone, R. Mignani and R. M. Santilli,
J. Phys. G: Part. Phys. vol. 18, L141-L144 (1992)
that are of the same order of magnitude of the values by Nielsen and Picek, Eqs. (5.26), (5.28).
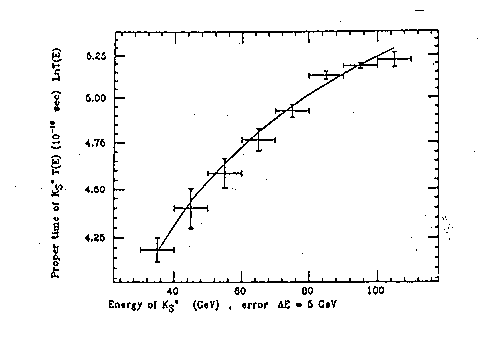
Figure 5.4: The exact plot done by Cardone et al (loc. cit.) of Aronson's experimental data (loc. cit.) via Santilli isometric on the anomalous behavior of the meanlife of Ko with speed in the energy range from 30 to 100 GeV.
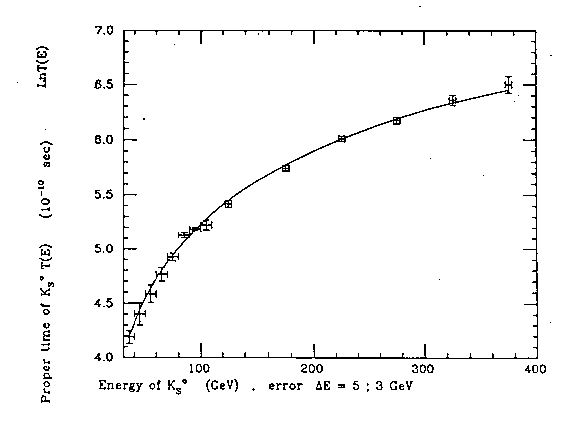
Figure 5.5. The exact plot done by Cardone et al (loc. cit.) of the seemingly divergent experimental data of both Aronson's and Grossman's experimental data (loc. city.) via Santilli's isometric in the energy range from 30 to-400 GeV. These plots provided an experimental confirmation of Santilli's isolaw (5.18) in the interior of kaons with numerical values (5.29)-(5.39). Note the clear emergence of a deviation from the Einsteinian law (5.16) despite its (claimed) recovering by Grossman's measurements. The experiments here considered are manifestly fundamental because they establish deviations from the Minkowskian spacetime in the interior of hadrons in favor of Minkowski-Santilli isospacetime
due to its direct universality. In turn, the generalization of the basic geometry within hadronic matter has far reaching implications in particle physics, nuclear physics, astrophysics and other fields, including new clean energies. As shown in subsequent chapters, the tests here considered also signal the initiation of a new technology based, for the first time, on strong interactions, an occurrence simply impossible under the exact validity of special relativity in the interior of hadrons.
and related isomathematics. Despite this exact reconstruction, one should note that the conventional Lorentz transformations are necessarily broken for all deformed metrics. Only the Lorentz symmetry remains exact, although realized in a more general way.
Yu. Arestov, R. M. Santilli and V. Solovianov,
Found. Phys. Letters Vol. 11, 483-493 (1998)
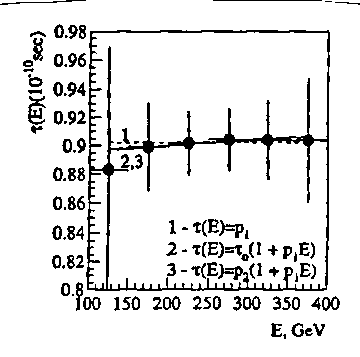
Figure 5.6: A view of three plots made by Arestov et al. (loc. cit.) via the use of Grossman's statistics of tests (loc. cit.) on the energy dependence of the meanlife of the neutral kaon on the energy showing the dominance of the PC violation selected in Grossman's tests to such an extent to show an apparent lack of dependence of the meanlife on energy, while the same dependence is clear in the different parametrization selected in the data elaborations by Aronson (loc. cit.) as well as Aronson (loc. cit.). These and numerous other equivocal aspect cast serious shadows on the acceptance for publication of the paper by Grossman's et al without a more serious scrutiny.
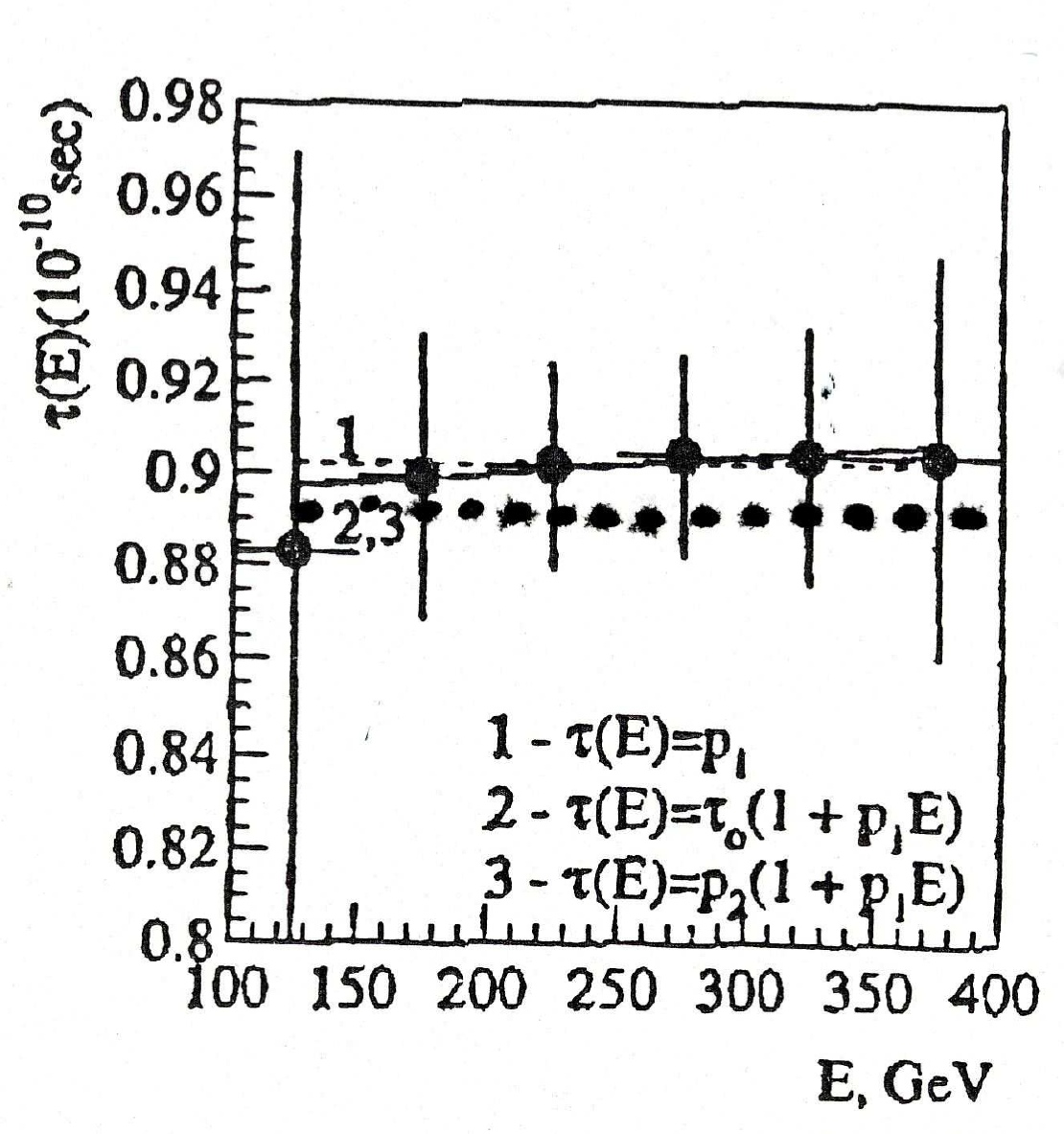
Figure 5.7: A plot of the same data as those of Figure 5.6 run by Santilli in HMMC Volume IV via the use of d parameters different than those used by Aronson et al. showing the extremely unsettled character of claimed "experimental results" when obtained via the use of ad hoc parameters and functions fit from the experimental data within the context of established doctrines. In fact, Santilli's plot shown in this figure obtained via the use of the same experimental data as those used by Aronson et al show clear deviations from special relativity expected in any case for an irreversible decay process due to the strict reversibility of the assumed theory.
Also, in the selected number of events, both Grossman's and Arestov's fits achieve a good mean
value of the hidden parameter
determining the energy dependence in the neutral kaon decays.
However,
the error bars differ strongly, although both results for the same fitting values
remain statistically insignificant, even in the selected sample of
events. Therefore,
the 100 % error bar in Arestov's plot illustrates the insufficiency of Grossman's tests quite clearly, since such error permits
manipulations of the selection procedure aiming at achieving a predetermined
result.
The tests by Grossman's et al (loc. cit.) were finally re-examined by Santilli in the monograph
Hadronic Mathematics, Mechanics and Chemistry, Volume IV,
R. M. Santilli, International Academic Press (2008)
where one can see the possibilities of large differences in the ''experimental results" claimed by Grossman et al. (loc. cit.) via even minimal changes in only one out of a variety of parametrizations, cut offs, and other manipulations used to achiieve compliance with Einsteinian doctrines, thus voiding Grossman's tests of any conclusive character on all serious scientific grounds.
In conclusion, the confirmation of special relativity within the hyperdense media inside the kaons claimed by Grossman et al (loc. cit.) has no conception or epistemological credibility; the claim is far from being resolutory in their energy range of 100 to 400 GeV due to an excessive number of equivocal theoretical and phenomenological manipulations of the raw experimental data, besides having insufficient statistics and excessive error; and, even assuming that the claim is eventually confirmed by future tests, the results are inapplicable to Aronson's tests in the different range of 30-100 GeV.
The exact fit by Cardone et al (loc. cit.), and Arestov et al. (loc. cit.) of experimental data by Aronson and Grossman constitutes experimental verifications on the following predictions by Santilli isorelativity:
1) Photons propagate inside kaons at speeds bigger than that in vacuum,
2) The maximal causal speed inside kaons is bigger than the speed of the local photons (as it occurs for water, Section 3.10, Isoaxiom I)
3) The kaons intrinsic time t* (isotime) is different than our own time t, and it is given by
4) The time isounit decreases with the increase of the density, as shown by the data in the transition from pions to kaons, thus predicting that the isotime for gravitational singularities is null.
5) Photons that may be emitted within the interior of hadrons reach the outside vacuum either redshifted or blueshifted depending on the density of the hadron considered (see Isoaxiom IV).
5.2C. Experimental verifications with arbitrary local causal speeds
A central feature of relativistic hadronic mechanics is that of predicting maximal causal speed that can be either smaller or bigger than the local speed of light depending on the characteristics of the medium at hand. The experimental evidence establishing the impossibility of reducing light to photons propagating in vacuum, thus at the speed c irrespective of the medium of propagation, is studied later on in this chapter. In this section we provide illustrations of maximal causal speeds smaller and bigger than the speed of light in vacuum.
As it is well known, all action-at-a-distance interactions cannot accelerate matter beyond the speed of light in vacuum, since the mere achievement of the speed of light would require infinite energy. For the case of maximal causal speeds within physical media, the situation is different for several reasons. To begin, the speed of light is no longer the maximal causal speed within physical media, as it is well established for water where ordinary electrons can travel faster than the local speed of electromagnetic waves. Causality is preserved by Santilli isorelativity precisely because its maximal causal speed in water is bigger than the local speed of light, and turns out to be given by the speed of light in vacuum due to the homogeneity and isotropy of the medium,
In turn, the above values for Vmax and C = c x b4 assure the validity of the isotopic sum of speed of light as well as all Santilli isoaxioms, as one can verify.
Furthermore, motion within physical media occurs under the additional presence of contact interactions that have no potential energy, thus being able to accelerate particles without any local energy consideration, as it is the case of a leaf accelerating in air. When strong interactions are assumed to have a contact, nonpotential component, they can accelerate particles (within hyperdense media) faster than the local speed of light, precisely as it is the case for electrons moving in water at speed bigger than the local speed of light, but always smaller than the maximal causal speed. These ideas were published for the first time by Santilli in the following paper of 1982
Can strong interactions accelerate particles faster than the speed of light?
R. M. Santilli,
Lettere Nuovo Cimento Vol. 33, pages 145-153 (1982)
The above hypothesis was studied in the 1980s by various authors but subsequently ignored due to organized interest intent in maintaining the dominance of Einsteinian doctrines for all possible conditions existing in the universe.
Subsequently, G. Nimtz and other experimentalists provided evidence of the propagation of light within certain guides at speeds faster than that in vacuum,
A. Enders and G. Nimtz, J. Phys. France Vol. 2, 1693 (1992).
G. Nimtz and W. Heitmann, Progr. Quantum Electr. Vol. 21, 81 (1997),
to such an extent that an entire Beethoven symphony was transmitted at speeds C measured as being bigger than c.
Unfortunately for scientific knowledge, organized interests on Einsteinian doctrines have dismissed these experiments via all sort of theoretical arguments, in full knowledge that experimental results can solely be dismissed in a credible way via counter-experiments. As an illustration, by searching under "Superluminal speeds" one can find in wikipedia (http://en.wikipedia.org) a very long list of attempted reinterpretation of speeds bigger than c in a way compatible with Einsteinian doctrines, while carefully avoiding even the quotation, let alone the addressing of Nimtz and other experiments. Most unreassuring is the presentation of numerous extremely ephemeral, thus implausible interpretations compatible with Einsteinian doctrines, while carefully ignoring, at least for completeness, the direct interpretation of the experiments as establishing within physical media indeed speeds bigger than c, thus voiding the entire long presentation of any serious scientific content or credibility. The same presentation at wikipedia dismisses speeds of light within physical media smaller than that in vacuum via equally esoterical arguments while carefully avoiding the five experimental facts outlined in Figure 6.1.
As we shall see, the validity within a hadron of Santilli iso-Minkowskian geometry and the Lorentz-Poincare'-Santilli isosymmetry is truly fundamental for the scientific study and industrial development of new clean energies. Despite their transparent scientific and societal importance, all major particles laboratories in the U. S. A., Europe and Russia have refused to conduct resolutory experiments on the behavior of the meanlives of unstable particles with speed following formal petitions by Santilli as well as numerous other concerned scientists.
The unreassuring character of the 20th century physics is identified in its full light by the fact that, despite the indicated equivocal aspects well known to experts to qualified as such, the fundamental experimental resolution of the exact or merely approximate validity of Einsteinian doctrines for the interior of hadrons, not only has remained unsolved since Aronson's tests of 1987, but the editors of major physical societies have rejected qualified dissident papers since 1987 on grounds that "Grossman's experiments have confirmed the validity of special relativity in the field," and the repetition of the test has been systematically refused by all particle physics laboratories in the world despite accorate appeals by Santilli and others. Similar unresolved fate occurred since 1992 for the confirmation or denial Nimtz speeds bigger than that of light via counter-experiments, rather than equivocal theological manipulations solely damaging their author and their country, rather than conducting any physical research of any value.
Since, on one side, new clean energies are crucially dependent on deviations from the exact validity of special relativity inside hadrons (Chapter 9), and since, on the other side, organized interests have systematically prevented or otherwise jeopardized the experimental verification of basic physical laws within hadrons, the only possible conclusion is that, as it was the case for Rauch's fundamental interferometric experiment, no serious advancement toward new clean energies is possible without concerned people first addressing issues of scientific ethics and accountability in particle physics.
5.2D. Experimental verification via the Bose-Einstein correlation
To complete our few illustrative cases of the experimental verification of hadronic mechanics in particle physics, we present the numerically exact and time invariant representation of the Bose-Einstein correlation from first unadulterated axioms under the reconstruction of the exact Lorentz-Poincare' symmetry on isospace over isofields. This historical result was first achieved by Santilli in 1992 in the memoir
Nonlocal formulation of the Bose-Einstein correlation within the context of hadronic mechanics
R. M. Santilli,
Hadronic J. Vol. 15, pages 1-134 (1992)
The verification was re-examined by F. Cardone and R. Mignani in the 1996 paper
Metric description of hadronic interactions from Bose-Einstein correlation
F. Cardone and R. Mignani,
JETP Volume 83, pages 10434448 (1996)
A comprehensive recent treatment was then provided by Santilli in his 2008 monograph that is herein adopted
Hadronic Mathematics, Mechanics and Chemistry, Volume IV,
R. M. Santilli, International Academic Press (2008)
Hadronic mechanics has been built for quantitative treatments of the nonlocal-integral character of the hadronic structure and the
strong interactions at large. Therefore, the fundamental verifications of the new mechanics are those directly dealing with nonlocal interactions.
Among various possible experimental verifications of this type, an important verification is that with the Bose-Einstein correlation here referred to the collision of protons and antiproton at high or low energy, their annihilation forming the so-called "fireball," and the subsequent emission of a number of unstable massive particles whose final product is a set of correlated mesons (see Figure 5.8 below).
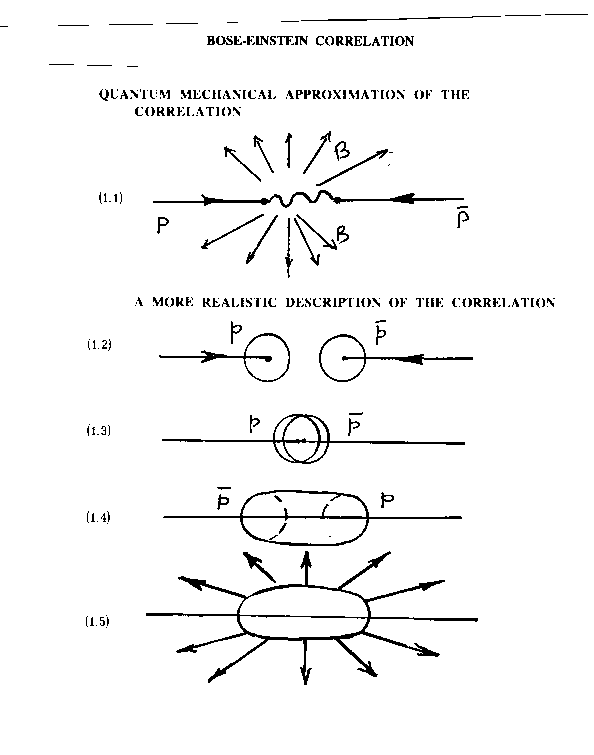
Figure 5.8: A schematic view of the Bose-Einstein correlation originating in proton-antiproton annihilations. The top view depicts the event as permitted by quantum mechanics, that is, with the necessary abstraction of protons and antiprotons as massive points, in which case no correlation is conceptually or technically possible (see the text). The lower views depict the event as described by the covering hadronic mechanics, according to which the proton and the antiproton are represented with their actual, extended, non-spherical and deformable shape. The particles first coalesce, then they annihilate and form the so-called "fireball," namely, a spheroid ellipsoid whose prolate character depends on the energy of the particles. The fireball then decays into numerous unstable hadrons whose final product is given by correlated mesons released in all space directions.
Evidently, the approximate validity of quantum mechanics for the Bose-Einstein correlation is beyond scientific doubt. However, any firm belief on the exact character of quantum mechanics for the event here considered is a scientific misconduct, particularly if proffered by experts in the field.
In fact, the Bose-Einstein correlation is necessarily due to nonlocal-integral effects originating in the deep overlapping of the wavepackets of protons and antiprotons. The mathematical foundations of quantum mechanics (such as its topology), let alone its physical laws, are inapplicable for any meaningful representation of said nonlocal interactions (those occurring in a volume that, as such, cannot be consistently reduced to a finite set of isolated points as requested by quantum mechanics).
The fundamental quantity needed for the representation of experimental data on the Bose-Einstein correlation, the two-point correlation amplitude (see below), is irreconcilably incompatible with the basic axioms of quantum mechanics when expressed in a form representing the experimental data.
To clarify this occurrence, let us recall that the basic quantum mechanical axiom of expectation values of a Hermitean, thus diagonal operator A (observable) solely permits structures of the type
By comparison, as expected to be known by experts, a quantitative representation of the Bose-Einstein correlation requires non-null cross terms of the type
that are impossible for the quantum axiom of expectation value for Hermitean, thus observable operators.
For the case of the two-point correlation amplitude, the maximal number of parameters admitted by quantum mechanics is, therefore, two, while any representation of experimental data requires four parameters of totally unknown physical origin and meaning, called the "chaoticity parameters." In fact, the rigorous application of the unadulterated axioms of relativistic quantum mechanics predicts the following two-point correlation function
where N is a renormalization constant, r is the radius of the fireball and q the relative four-momentum of the proton-antiproton system. However, the above expression is dramatically far from experimental data.
A chain of adulterations of the exact expression (5.45) were then ventured in the literature in order to achieve a fit of experimental data while still claiming exact validity of quantum mechanics. A first adulteration is given by the expression
where P is an ad hoc "chaoticity parameter," introduced without any physical motivation or origin.
Expression (5.46) also resulted in being excessively far from experimental data. Therefore, additional adulterations became necessary with expression of the type
The latter expression too resulted in being basically insufficient to represent experimental data and, therefore, the chain of adding arbitrary parameters of unknown physical origin or meaning was continued to salvage quantum mechanics, by reaching in this way the indicated need for four chaoticity parameters, while in reality crossing the limits of applicability of quantum mechanics.
It is then clear to ethically sound scholars that, rather than confirming the validity of quantum mechanics as claimed for political reasons, the four chaoticity parameters establish instead the deviation of quantum mechanics from the experimental evidence of the Bose-Einstein correlation.
After studying the problem for years, Santilli (loc. cit.) proposed in 1992 the following treatment of the Bose-Einstein correlation via relativistic hadronic mechanics for the following reasons:
i) Relativistic hadronic mechanics has been built precisely for the quantitative treatment of nonlocal-integral interactions occurring in the Bose-Einstein correlation;
ii) The basic axioms of relativistic hadronic mechanics have been built to admit the needed cross terms in the expectation values of Hermitean operators, which cross terms are merely permitted when the isotopic element T is Hermitean but has non-diagonal elements,
iii) Relativistic hadronic mechanics reconstructs the exact Lorentz-Poincare' symmetry for the Bose-Einstein correlation because all nonlocal-integral effects are embedded in the generalized unit;
iv) Relativistic hadronic mechanics is the only known generalized mechanics outside the class of unitary equivalence of quantum mechanics that achieves invariance over time, thus avoiding the catastrophic physical and mathematical inconsistencies of nonunitary theories (Section 3.7);
v) As it was the case for the behavior of the meanlife with speed, relativistic hadronic mechanics is directly universal, thus including as particular cases all possible nonunitary generalizations of quantum mechanics.
Santilli representation of the Bose-Einstein correlation via relativistic hadronic mechanics can be outlined as follows. The new mechanics permits a direct representation (i.e., a representation via the isometric itself) of the actual shape of the fireball with the space characteristic quantities b1-2, b2-2, b3-2 representing the semiaxes of the spheroid ellipsoid, as well as of the density of the fireball via time characteristic quantity b4-2, resulting in Santilli's isounit, isotopic element and isometric (Section 3.10)
where m = Diag. (1, 1, 1, -1) is the conventional Minkowski metric.
The above diagonal expression is insufficient for the proton-antiproton correlation due to the need for nonlocal-integral interactions as well as of the indicated cross terms. Therefore, the complete isominkowskian metric is given by the above expression for m* multiplied by the following nondiagonal Hermitean matrix
where C11 and C22 are real valued, C12 = C21†, and the four Cs are given by all possible integrals in the inner product of wavefunction 1 for the proton and 2 for the antiproton (see Santilli, loc. cit., for brevity), thus resulting in the needed four contributions.
The isotopies of the conventional relativistic derivation yield the following Santilli two-point isocorrelation function
where qt is the momentum transfer needed to fit experimental data, m* is expression (5.51) and K has the following form
where the normalization to 3 is requested to admit a consistent relativistic limit.
By using isocorrelation amplitude (5.53), Santilli predicted the following maximal and minimal values
as well as the following maximal values for the fourth characteristic quantity (density of the fireball)
Therefore, relativistic hadronic mechanics predicts that the speed of photons inside the Bose-Einstein fireball is bigger than that in vacuum,
and that the intrinsic time of the fireball (isotime) is decreased with respect to our time
All the above theoretical predictions resulted in being confirmed by the fit of the experimental data subsequently conducted by Cardone and Mignani (loc. cit.) resulting in the following numerical values (see Figure 5.9)
Note the very elongated character of the fireball established by the experimental values of its semiaxes nk2, k = 1, 2, 3. Note also that the density of the fireball, b42 = 2.732 is bigger than 1, thus establishing that the speed of photons within the fireball is bigger than that in vacuum.
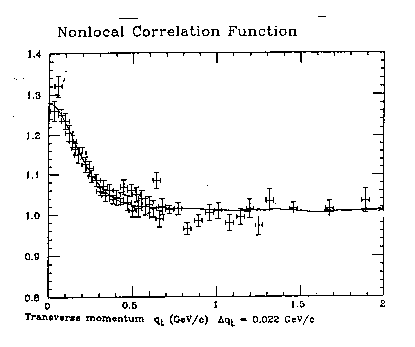
Figure 5.9: A reproduction of the excellent fit of the two-point isocorrelation function with experimental data on the Bose-Einstein correlation at very high energy from the celebrated UA1 experiments at CERN, first published by Santilli in 1991 (loc. cit.) and then re-examined by Cardone and Mignani in 1996 (loc. cit.). As one can see, the fit is a clear experimental verification of the validity of Santilli isorelativity in the interior of the proton-antiproton fireball. The fit reproduced in this figure may well result in being, in due time, the first experimental evidence on the ultimate nonlocality of the structure of the universe, with consequential needs for a suitable generalizations of contemporary local-differential mathematics, geometries, mechanics and relativities.
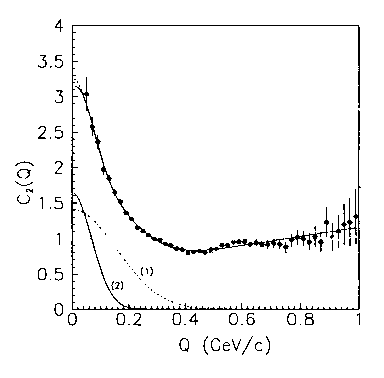
Figure 5.10: Another exact fit of the experimental data on the Bose-Einstein correlation for proton and antiproton annihilation, this time, at low energy. Curves indicated with 1 and 2 represent the fits with quantum models. Their dramatic deviation from experimental data is sufficient to disqualify any claim on the exact validity of quantum mechanics for the Bose-Einstein correlation that, unfortunately, has been rather widespread during the physics of the second half of the 20th century.
5.2E. Characterization of hadronic media
The above fits provide a major experimental verification of the following aspects:
I) The predictions by relativistic hadronic mechanics are confirmed with an exact fit of the experimental data;
II) The fits of experimental data confirm the maximal value 1.67 and minimal value 1 of the two-point isocorrelation function;
III) The experimental fits confirm the theoretical prediction for the value of the density of the proton-antiproton fireball;
IV) The experimental fits confirm the nonlocal, nonpotential and nonunitary nature of the correlation at the very foundation of hadronic mechanics;
V) The fits confirm the validity of Santilli isorelativity and related isometric for the interior of the proton-antiproton fireball;
VI) The fits confirm the capability by relativistic hadronic mechanics of reconstructing the exact Lorentz-Poincare' symmetry at the isotopic level for the proton-antiproton annihilation;
VII) The fits confirm that the speed of photons within hyperdense hadronic media is bigger than their speed in vacuum,
and that, from Isoaxiom IV, they are blueshifted in their propagation inside the fireball (acquire energy),
where k is the direction of emission, with consequential redshift for propagation within media of light density (loss of energy to the medium), a feature that allowed Santilli to eliminate dark energy as we shall see later on in this chapter;
VIII) The fit establish that the time in the interior of the fireball is slower than our time
thus yielding a null time for the interior of a gravitational singularity, an important feature for cosmology as we shall see later on in this chapter;
IX) The fits finally confirm Isoaxiom I according to which, for the considered fireball, the energy equivalence of the fireball is bigger than that predicted by special relativity,
a feature that allowed Santilli to eliminate dark energy, as we shall see later on in this chapter.
When the above experimental verifications are joined with those of the preceding sections and those of the following chapters, the validity of Santilli's isorelativity and relativistic hadronic mechanics emerge rather forcefully.
Independently from all the above, the reader should know that the most important single result of this section is that the numerical value of the density of hadronic matter provided by the experimental data on the proton-antiproton fireball has resulted to be crucial for the first quantitative representation of the synthesis of the neutron as occurring in stars from protons and electrons outlined in the next chapter.
5.3. EXPERIMENTAL VERIFICATIONS IN NUCLEAR PHYSICS.
5.3A. The unreassuring condition of 20th century nuclear physics.
Following the historical achievement of the numerically exact representation of all experimental data on the hydrogen atom, the 20th century nuclear physics has been developed under the condition of achieving full compliance with quantum mechanics. This occurrence has created an unreassuring condition of this important field of scientific knowledge because the dramatic physical differences between atomic and nuclear structures suggest deviations from quantum mechanics in the transition from the former to the latter structures, as established by the following insufficiencies identified by Santilli in numerous of his writings:
1) The Galilean and Lorentz-Poincare' symmetries of atomic structures cannot possibly be exactly valid for nuclear structures because said symmetries crucially depend on the Keplerian character of the structure with a Keplerian center, while, as Santilli stresses nuclei do not have nuclei. The proof of the inapplicability (rather than violation) of the conventional spacetime symmetries for the structure of nuclei can then be done by a first year graduate student (see Figure 5.11).
The absence of a Keplerian structure in nuclei was a primary motivation for Santilli to build his isotopic covering of the Galilei and Lorentz-Poincare' symmetries. In fact, such isotopies are based on the additional presence in interior structural problems of additional contact, zero-range nonpotential interactions whose primary implication is precisely that of "glueing" all constituents together, thus assuring the absence of a Keplerian nucleus.
Of course, the approximate validity of quantum mechanics in nuclear physics is and remains beyond doubt. However, when the basic quantum symmetries are no longer exact, the lack of exact character of quantum mechanics is also beyond doubt, the only debatable aspect being the selection of the appropriate generalization.
This is a truly central point of all of Santilli studies, as well as of this presentation, because, as shown in details in Chapter 9, the expected deviations from quantum mechanics, no matter how small, permit the conception and development of basically new nuclear forms of energy that are inconceivable under the current assumption of the exact validity of quantum mechanics in the field.
Figure 5.11: A visual evidence of the impossibility for quantum mechanics to be exactly valid in nuclear physics voiced by Santilli in numerous of his writings: the fact that "nuclei do not have nuclei," thus causing the breaking of the fundamental Galilean and Lorentz-Poincare' symmetries of quantum mechanics (see also Figure 1.2). The impossibility for quantum mechanics as being exact for the nuclear structure is then beyond credible doubt.
2) While quantum mechanics has achieved an exact representation of all features of the hydrogen atom, the same discipline has failed to reach a meaningful representation of the simplest possible nucleus, the deuteron, with embarrassing deviations for heavy nuclei, such as the zirconium.
In fact, following about one century of failed attempts, quantum mechanics has been unable to represent some of the basic features of the deuteron, such as its spin, stability, rest energy and other basic features (see Chapter 8).
Lacking an exact representation of experimental data from unadulterated first principles, any belief of the exact character of quantum mechanics in nuclear physics is outside the boundaries of serious science.
3) Quantum mechanics has been unable to provide any explanation of nuclear magnetic moments, as a result of which, the best treatises of 20th century nuclear physics merely list the values of nuclear magnetic moments between minima and maxima (see Figure 5.12).
Il should be stressed that quantum mechanics has been unable to represent the magnetic moment of the simplest possible nucleus, the deuteron, where about 1% remains missing despite all possible relativistic corrections.
The simplest possible interpretation of nuclear magnetic moments is Santilli's deformation of the shape of protons and neutrons under nuclear forces with consequential mutation of their intrinsic magnetic moments, but it could not be adopted by the 20th century mainstream nuclear physics because causing the exiting from the boundary of quantum mechanics.
Figure 5.12: Additional evidence of the lack of exact character of quantum mechanics in nuclear physics given by experimental data on nuclear magnetic moments that do not follow quantum predictions, and are instead comprised between certain maximal and minimal values partly reproduced in this figure from known nuclear sources.
4) Quantum mechanics has failed to achieve a full understanding of the nuclear force, despite about one century of attempts. This is essentially due to the pre-determined intent of rendering the representation compatible with quantum theories, as a result of which the sole admitted forces are of potential type.
In turn, the sole use of a potential has turned nuclear forces into a distressing scientific field, since the addition of about forty potentials in the nuclear force, Eq. (1.6), has failed to achieve any resolution.
It should be noted that the admission of a contact interaction among nuclear constituents, as established by evidence, could not be adopted by 20th century nuclear physics because it would have implied the exiting from the class of unitary equivalence of quantum mechanics, a line of research opposed by 20th century leading nuclear circles around the world.
5) Quantum mechanics cannot possibly be exact for nuclear fusions due to the strict reversibility of the former compared to the strict irreversibility of the latter. One of the best kept secrets in Ph. D. courses in nuclear physics is that the quantum mechanics predicts a finite probability for the "spontaneous" disintegration of a nucleus following its synthesis, Eq. (1.4).
An argument used by mainstream nuclear physics to bypass the above insufficiency is that "quantum mechanics works well for nuclear fissions," a statement that is indeed correct, as established in any case by the good operation of nuclear power plants based on nuclear fission.
The equivocal aspect, particularly when not identified by experts, is the lack of indication of the dramatic differences between nuclear fissions and fusions as stressed several times by Santilli in his writings, Even though manifestly irreversible, nuclear fissions produce debris that, moving in vacuum, can be well abstracted as being point-like, thus permitting quantum mechanics to provide a good approximation. By contrast, no point-like abstraction of nuclei is possible for any, minimally credible representations of nuclear fusions, in which case the inapplicability of the theory is beyond doubt, as established in any case by over half a century of failed attempts to achieve industrially valuable "cold" and "hot" fusions (following an overall investment in excess of one billion dollars).
Santilli conceived hadronic mechanics in 1978 and headed its construction as well as verification precisely for the resolution of nuclear insufficiencies 1) to 5) of quantum mechanics. A minimal knowledge of the field can be claimed only following a technical understanding that hadronic mechanics is the only covering of quantum mechanics providing a resolution of the above insufficiencies in a a way form invariant over time. Santilli's use of hadronic mechanics in nuclear physics is based on:
I) The termination of the sole use of potentials or Hamiltonians;
II) The sole representation with a Hamiltonian of interactions with an assured at-a-distance character,
III) The representation of all remaining interactions, features and effects with isounits of the type
where: the space characteristic quantities bik-2 = nik2, i = 1, 2, 3, permit, for the first time, a direct representation of the actual, nonspherical and deformable shape of the charge distribution of nucleons, or of a nucleus as their collection; the time characteristic quantity b4k-2= n4k2 permits, also for the first time, a direct representation of the density of nucleons, or of the nucleus; the function F permits, again for the first time, a consistent and time invariant representation of nuclear interactions that are nonlinear in the wavefunction, nonlocal (of integral type) and contact (nonpotential) character; and the hadronic representation is restricted by the condition Lim I*r >> 1 Fermi.
under which hadronic mechanics recovers quantum mechanics uniquely and identically, as now well known.
The consistency of hadronic mechanics for nuclear structures and their reactions is then assured by various properties hereon assumed to be known, such as: the preservation of Hermiticity under isotopies as a result of which all quantum mechanical observables remain so under hadronic mechanics; the preservation under isotopies of the generators of quantum spacetime symmetries as a result of which all conventional total quantum mechanical conservation laws remain fully valid under treatment by hadronic mechanics; and other features (see Section 3.11).
A general presentation of the specialization of hadronic mechanics for nuclear structures is available from the memoir
Nuclear realization of hadronic mechanics
and the exact representation of nuclear magnetic moments
R. M. Santilli,
Intern. J. of Phys. Vol. 4, 1-70 (1998)
Santilli quite intriguing reconstruction of the exact SU(2)-isospin symmetry in nuclear physics is available from the paper
Isorepresentation of the Lie-isotopic SU(2) algebra with
application to nuclear physics and local realism,
R. M. Santilli,.
Acta Applicandae Mathematicae Vol. 50, 177-190 (1998)
The first known time invariant Lie-admissible treatment of irreversible nuclear processes is available from the paper
A possible Lie-admissible time-asymmetric
model of open nuclear reactions,
R. M. Santilli,
Lettere Nuovo Cimento Vol. 37, 337-344 (1983)
while a comprehensive Lie-admissible treatment of irreversibility is available from the recent memoir
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
A comprehensive study is available in Santilli's five volumes
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V:
R. M. Santilli, International Academic Press (2008)
5.3B. Experimental verification with nuclear magnetic moments.
The first historical hypothesis for the correct interpretation of the anomalous behavior of nuclear magnetic moments dates back to the time of Fermi, Segre, and others in the 1940's. The hypothesis then propagated to various treatises in nuclear physics in the first half of the 20th century. For instance, in the treatises in nuclear physics by Blatt and Weisskopf (not quoted here because it is excessively known) one can read on page 31:
It is possible that the intrinsic magnetism of a nucleon is different when it is in close proximity to another nucleon.
The study of this so plausible a hypothesis, was abandoned in the second half of the 20th century when researchers understood that alterations of the intrinsic characteristics of nucleons are strictly prohibited by quantum mechanics, as indicated in Section 5.1.
A quantitative isotopic representation of the deuteron magnetic moment
The representation was then expanded in the memoir herein adopted
Nuclear realization of hadronic mechanics
and the exact representation of nuclear magnetic moments
The study is essentially based in the use of the Dirac-Santilli isoquation (Section 3.11Q) that characterizes the isotopy of the conventional quantum mechanical treatment of nuclear magnetic moments. This settings leads to the following total isonuclear magnetic moments expressed for simplicity along the third axis
It is easy to see that the above model provides a numerically exact, quantitative resolution of total nuclear magnetic moments that had remained unachieved for about a century.
Consider first the case of the deuteron, that is a p-n bound state in triplet S-state (L = 0), the state with L = 1 being unallowed by parity (that is preserved under isotopies). We then have the following quantum mechanical (QM) and experimental values of the deuteron magnetic moment
By comparison, we have the following deuteron magnetic moment as exactly represented by Santilli via hadronic mechanics (HM)
The reader should be aware that Santilli's hypothesis on the mutation of the intrinsic characteristics of particles was based precisely on the above historical legacy. Following the prior construction and verification of hadronic mechanics, the first known exact representation of nuclear magnetic moments was presented by Santilli at the meeting
R. M. Santilli,
in "Proceedings of the International Symposium 'Dubna Deuteron-93'", Joint Institute for Nuclear Research, Dubna, Russia (1994)
R. M. Santilli,
Intern. J. of Phys. Vol. 4, 1-70 (1998)
where L (S) represents the angular momentum (spin), and the g-quantities are characterized by
To a good approximation, the density b4k of individual nucleons can be assumed to be the same for all nucleons. Santilli selects value (5.65) because it represents the density of nucleons as derived from other fits, by reaching in this way the expression
where we have assumed in first approximation that the isoproton and the isoneutrons experience the same mutation.
Note that the quantum mechanical representation is in excess of the experimental value. Therefore, the exact representation requires a reduction of the above theoretical values. In turn, this implies the prediction of a prolate spheroidal deformation of nucleons (in which the rotation occurs along the symmetry axis), because an oblate deformation would imply an increase of the magnetic moment (classically due to the increase of the tangential speed of the charge distribution).
The remaining two semiaxes of the isonucleons (evidently assumed to be spheroid ellipsoids due to spin) can be identified via the condition used earlier that mutations of shape must conserve the density (or volume) of the nucleon. Therefore, Santilli introduces the condition
from which he obtains the value of all semiaxes of the two isonucleons in the deuteron
As one can see, hadronic mechanics achieves an exact and invariant representation of the deuteron magnetic moment, by confirming the prediction that the alteration is prolate. The physical interpretation of the representation is so simple to be trivial (see Figure 5.13 below). The above model should be refined via different mutations of the isoproton and the isoneutron, evidently expected from their different values of charge and other features. This study is left to the interested reader.
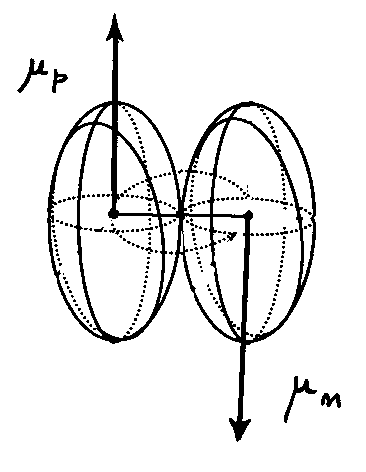
Figure 5.13: A schematic view of the structure of the deuteron according to Santilli. The fundamental assumption is the rather natural expectation expressed by the founders of nuclear physics that, when coupled into the deuteron, protons and neutrons experience a deformation of their shape when isolated in vacuum (assumed to be perfectly spherical from Dirac's equation). The deviation of the experimental value of the total magnetic moment of the deuteron from the quantum mechanical predictions (about 1% in excess) then yields a numerical characterization of the deformation of the nucleonic shape, that results to be prolate spheroid ellipsoids as depicted in the figure from values (5.92). Note that the configuration of the figure is centrally dependent on Santilli's isosymmetris because the latter characterize the deuteron as a closed-isolated system with conventional Hamiltonian interactions and additional non-Hamiltonian contact forces, thus assuring the presence of a contact between the proton and the neutron as a condition to preserve the nuclear force.
The above results will be re-examined in Chapter 8 with a deeper structure model of the deuteron in which the neutron is reduced to its constituents.The extension of the above model to an exact representation of the magnetic moment of the tritium and all other nuclei is straighforward and it is left to the interested reader, jointly with refinements due to D-couplings, pionic currents and other aspects here basically inessential to illustrate the exact representational capability of hadronic mechanics compared to the approximate capabilities of quantum mechanics.
5.3C. Experimental verifications with the nuclear force
Additional, perhaps more important verifications of hadronic mechanics are given by its representation of the nuclear force. As recalled in Chapter 1, quantum mechanics solely allows the use of a Hamiltonian for the representation of all nuclear structures. Consequently, the sole possible time invariant representation of the nuclear force is that via potentials. After about one century of failed attempts, it is today known that such a representation is unable to provide an exact representation of the nuclear force, since the use of some 43 different potentials with 43 different parameters has failed to reach an exact result.
Santilli has truncated this sterile process of adding potentials to the kinetic energy because nuclear forces are of action-at-a-distance, potential type only partially, since their primary origin is of contact nonpotential character. In fact, experimental data on nuclear volumes compared to those on the volumes of the charge distributions of protons and neutrons (nucleons) established that, when members of a nuclear structure, nucleons are in conditions of partial mutual penetration of the hyperdense media in their charge distributions, resulting in an incontrovertible contact nonpotential interactions,
The only known time invariant representation of the nonpotential part of the nuclear force is that via Santilli isounit realized within the context of hadronic mechanics. Regrettably, we are not in a position to review this study because of its industrial implications for new clean energies preventing disclosure at this time. For a partial release of the studies, one may consult HMMC, Volume IV.
5.4. EXPERIMENTAL VERIFICATIONS IN CHEMISTRY AND SUPERCONDUCTIVITY
5.4A. Experimental verifications in chemistry
Chemistry constitutes one of the most important fields of experimental verifications of hadronic mechanics because the very notion of electron valence coupling is beyond a serious representational capability by quantum mechanics due to the presence in molecular structures of the interactions caused by deep wave-overlapping, not to mention the fact that identical electrons are predicted by quantum mechanics to repel each other and additional insufficiencies indicated in Chapter 1.
Chapter 4 has been devoted to the experimental verifications and applications of hadronic mechanics in chemistry as well as biology. We here merely mention for completeness the achievement by hadronic mechanics of the first known, numerically exact representation of molecular binding energies obtained from unadulterated first axioms without ad hoc parameters or "screening" functions fitted from the data, as well as other verifications.
5.4B. The unreassuring condition of 20th century superconductivity
As it was the case for particle physics, nuclear physics and chemistry, the condition of 20th century superconductivity was equally unreassuring because based on the unlimited applicability of quantum mechanics much beyond the limits of its conception and experimental verification, without any serious scrutiny.
There is no doubt that superconductivity has made major advances in recent decades. However, there is equally no doubt that superconductivity is currently at the stage of atomic physics before the discovery of the structure of atoms. In fact, superconductivity is based on electrons bonded in Cooper pairs, yet no quantitative model exists or is actually permitted by quantum mechanics for such pairs since, as it is the case for valence bonds, electrons are predicted by quantum mechanics to repel each other. More specifically, quantum mechanics does achieve an excellent representation of an ensemble of Cooper pairs, the quantum insufficiency here referred to is for the structure of one Cooper pair. Note that electrons in Cooper pairs are so deeply bonded/correlated to have been detected crossing potential barriers in said bonded form.
The central role of Cooper pairs in superconductivity is due to the fact that the total magnetic moment of a Cooper pair is dramatically smaller than that of individual electrons (due to the antiparallel alignment of the two electrons). Therefore, Cooper pairs experience much less resistance than individual electrons in their hopping from one atom to another in a conductor, thus permitting superconductivity (see Figure 14).
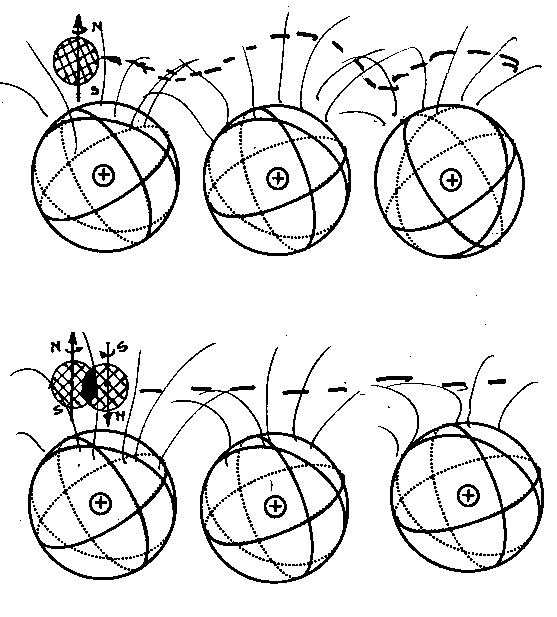
Figure 5,14: A schematic view of a conventional current of individual electrons (top view) and a superconducting current of Cooper pairs (lower view). The smaller electric resistance experienced by the latter as compared to that of the former current is due to the absence in the Cooper pair of an appreciable magnetic moment from its singlet structure, resulting in much smaller interactions with the atoms of the conductor. Note that we are here referring to a basically new current not yet industrially realized.
Due to the inability by quantum mechanics to permit an attractive force between two identical electrons, researchers were forced to introduce new interactions seemingly experienced by electrons that have no counterpart in other branch of physics. We are referring to the so-called phonons and related new electron-phonon interactions that are assumed as permitting said attractive bond. Inspection of all other branches of physics reveals that phonons exist in the sound theory, but not at the particle level, thus casting shadows in the actual existence of phonons beyond the level of a purely mathematical formulation. Alternatively, the lack of existence of electron-phonon interactions outside superconductivity casts doubts as to whether the conjecture of phonons will survive the test of time.
Above all, the stretching of the validity of quantum mechanics for systems for which it was not built for is best manifested by the exhaustion of predictive capacities by the quantum formulation of superconductivity. In fact, all theoretical predictions of increasing the superconducting temperature have been exhausted, while all advances are attempted via phenomenological trials and errors without a sound guiding theory.
As it was the case for preceding fields, the approximate character of quantum mechanics in superconductivity is beyond doubt. Equally beyond doubt is the need for a deeper theory capable of providing a quantitative structure model of the Cooper pair, representing the various aspects in a way compatible with experiments and exhibiting novel predictive capacities for further advances.
5.4C. Animalu's isosuperconductivity
The research reported in this section originated with Santilli's proposal in 1978 to build hadronic mechanics, particularly with Section 5 of the paper
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
providing the first known representation of a bound state of one electron and one positron at short distance with nonlocal, nonlinear and nonpotential interactions due to deep wave overlappings. In the papers
A. O. E. Animalu, Hadronic J. {\bf 16}, 411 (1993)
A. O. E. Animalu, Hadronic J. {\bf 17}, 349 (1994)
Animalu recognized that the strength of the attractive force of the new non-Hamiltonian interactions is such to overcome the Coulomb repulsion, and, therefore, be applicable also to the electron-electron correlation of the Cooper pair. By using Santilli's studies, Animalu then applied hadronic mechanics to produce the first known structure model of the Cooper pair and built a new theory today known as Animalu isosuperconductivity. Finally, Animalu and Santilli completed the structure model of the Cooper pair via hadronic mechanics in the paper
A. O. E. Animalu and R. M. Santilli, Intern. J. Quantum Chem. {\bf 26},175 (1995).
It is assumed the reader is aware of the fact that, according to hadronic mechanics the constituents of the Cooper pair are "isoelectrons" and not conventional electrons. As a matter of fact, it will soon become evident that, without the isotopic interpretation of particles, a structure model of the Cooper pair is impossible, thus confirming the basic limitations of quantum mechanics.
It is evident that we can only outline here some of the main aspects of Animalu's isosuperconductivity and its clear experimental verification. The first step is to exit from the class of equivalence of quantum mechanics. This task can be achieved via nonunitary transforms of Eqs studied in Section 3.11O.
Consider the Schroedinger equation for one electron with mass m and charge -e in the field of an identical electron
The image of the above equations under a nonunitary transform is given by
where e^ represents the wavefunction of the isoelectron, and D*r represent partial isoderivative (Part I).
However, the creation of Cooper pairs requires an "external trigger' (in the language of hadronic mechanics). Since identical electrons repel each other, and since the new attractive non-Hamiltonian interactions only occur at short distances of the order of 1 fm, without an external action identical electrons would never form the Cooper pair.
It is evident that the "trigger" for the formation of the Cooper pair must be constituted by positive charges. Animalu's studies of the issue have discovered that the needed trigger cxan be provided by Cuprate ions as well as other compounds. The latter are purely quantum mechanical (because they act for large distances as compared to the range of applicability of hadronic mechanics). Therefore, the interaction of Cuprate ions must be merely added to the short range hadronic state resulting in the expression
where the positive charge ze is the ionic valence and the conventional quantum nature is expressed by the lack of multiplication by I*. Note that one could equivalently write the quantum model and add the hadronic effects at short range by achieving the same results.
At this point Animalu selected the following realization of the isounit and isotopic element:
where e*up and e*down represents the wavefunction of the isoelectron with spin up and down, respectively, and edown represents the wavefunction of the ordinary electron.
Note that isounit (5.101) provides a direct representation of the new interactions caused by deep waveoverlapping of the wavepackets of the isoelectrons that are nonlocal because represented by the volume integral, nonlinear because depending on the wavefunctions in a nonlinear way, and nonpotential because of clear contact/zero range type not representable with a Hamiltonian.
Most importantly, readers should keep in mind the short range character of the above isotopic lifting since isounit (5.101) recovers the trivial unit I for all distances sufficiently greater than 1 fm for which the volume integral is null. Under these conditions hadronic mechanics recovers quantum mechanics uniquely and identically. Therefore, we are here presenting new correlations solely occurring at short distances where quantum mechanics is inapplicable, while recovering quantum mechanics identically for all longer distances. This point is important because it will eliminate the need for the conjecture of phonons as physical quantities.
In order to obtain an explicit structure equation for the Cooper pair, we use the following behavior
where the first expression is known from atomic physics, the second expression was identified in Ref. (38), and R represents the charge radius of the Cooper pair. After substitution in Eq. (5.4) and turning the isokinetic energy into a renormalization m' of the electron mass m (another standard procedure of hadronic mechanics), we obtain the differential equation
where one recognizes the familiar Hulten potential first identified in Santilli's 1978 proposal that also provided a detailed analytic solution of the above equitation whose main lines can be summarized as follows.
In essence, at short distances the Hulten potential behaves like the Coulomb potential by therefore absorbing the repulsive contribution by the latter and resulting into a very strong attractive force between the two idenmtical electrons in singlet couplings. In fact, at short distance Eq. (5.105) yields the following structure equation of the Cooper pair of isoelectrons
where K is the new constant (in lieu of the original V) absorbing the coefficient of the repulsive Coulomb force.
The solutions of equation (5.106) yields the familiar Hulten energy spectrum
where h represents h-bar.
5.4D. Experimental verification of Animalu's isosuperconductivity
Santilli [loc. cit.] identified the solution for the structure of the po via the introduction of the two parameters
reviewed in the next chapter. Animalu identified the solution for the Cooper pair via the parametrization for the ground state
where F is the Fermi energy of the isoelectron. Eq. (5.110) can be written in good approximation
where Tc is the superconducting temperature and qD is the Debye temperature.
Figure 5.15. Animalu's [loc. cit.] remarkable experimental verification of isosuperconductivity. The figure shows the plot between the theoretical prediction for the dependence of the superconducting temperature from the effective valence z of cuprate ions (continuous curve) and the experimental values on the "jellium temperature" for various compounds (solid dots).
Animalu then worked out several examples, such as
where the effective valence z varies from a minimum of z = 4.66 for YBa2Cu3O6.96, Tc = 91oK, to a maximum of z = 4.33 for YBa2Cu3O6.5, Tc = 20oK. The general expression predicted by Animalu isosuperconductivity for YBa2Cu3O6-x is given by
and it is in remarkable agreement with experimental data (see the figures below).
Figure 5.16: A reproduction of Fig. 5, p. 380 of Animalu [loc. cit.] showing the agreement between the prediction of isosuperconductivity for the doped 1:2:3 Cuprates and the experimental data.
K = h x w,where w can be interpreted as the (average) phonon frequency. Expression (5.113) can then be rewritten
where NV is the (dimensionless) electron-phonon coupling constant. The main results of Animalu's model can therefore be reformulated in terms of the electron-phonon interactions, as expected. However, as also expected, the conjecture of the phonon is replaced in the model with the new non-Hamiltonian interactions for the simple reason that phonons have not been independently detected in particle or other branches of physics.
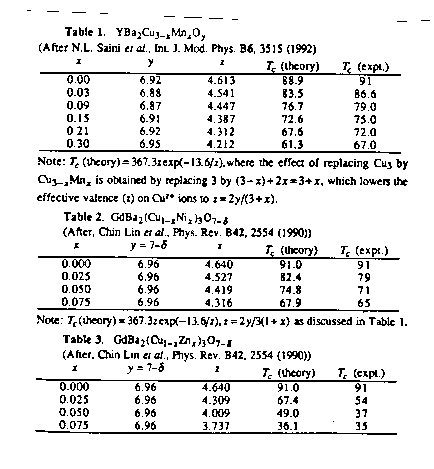
Figure 5.17: A reproduction of the tables of p. 379, ref. (169) illustrating the agreement between the predictions of isosuperconductivity with experimental data from other profiles.
5.4E. Initial basic laws of hadronic mechanics
By Combining the results and experimental verifications of Santilli's isochemistry studied in the preceding chapter and Animnalu's isosuperconductivity studied in this section, we are now in a position to identify the following three initial basic laws of bound states at short distances represented via hadronic mechanics (see Chapter 7 for additional laws) that were fully identified by Santilli in his original proposal of 1978 to build hadronic mechanics:
Basic law I of hadronic mechanics: Nonlinear, nonlocal and nonhamiltonian interactions due to wave-overlappings of spinning particles at short distances are always attractive when in singlet couplings and such to absorb repulsive or attractive Coulomb interactions, resulting in total strongly attractive interactions irrespective of wether the Coulomb interactions are attractive or repulsive.
As the reader will remember, the above law is at the foundation of the Santilli-Shillady strong valence that permitted the first exact representation of molecular data from unadulterated first principles. The same law is here verified in the structure of the Cooper pair in superconductivity. In the next chapter, we shall see that the same law is crucial for the synthesis of neutrons as occurring in stars from protons and electrons. Finally, the same hadronic law has a truly crucial role for the conception, and industrial development of a basically new form of controlled nuclear fusions at intermediate energies.
Basic law II of hadronic mechanics: Nonlinear, nonlocal and nonhamiltonian interactions due to wave-overlappings of spinning particles at short distances are always strongly repulsive when in triplet couplings irrespective of whether the Coulomb interactions are attractive or repulsive.
The best way to see Laws I and II is that originally used by Santilli for their derivation, and of is known as the "gear model." In fact, ordinary gears can only be coupled in singlet, while the attempt of coupling them in triplet causes strong repulsive forces, or the breaking of the teeth.
In essence, Santilli's 1978 argument is that particles are not points, but extended, and the interior of their wavepackets or charge distribution is not empty, but filled up with a dense physical medium. Therefore, the axioms of quantum mechanics (when used without adulteration via arbitrary functions fitted from the data) predict no difference between singlet and triplet couplings. By contrast, hadronic mechanics represents the actual extended shape of particles and their density, resulting in the unavoidable Basic Laws I and II.
Basic law III of hadronic mechanics: Bound states of particles due to wave-overlappings at short distances in singlet coupling suppress the atomic spectrum of energy down to only one possible level, a property called "hadronic suppression of the atomic energy spectra."
The mechanism of the above suppression is to the finite character of the number of energy levels admitted by the Hulten potential combined with the fact that all known fits of the solutions to experimental data reduce such a finite spectrum to only one energy value, that of the considered state.
The above property illustrates the dramatic structural differences between quantum and hadronic mechanics and it is forcefully verified in various fields of physics. To begin, the idea that valence electron bonds have a spectrum of energy levels of atomic type has no physical value or credibility since the valence bond is one and only one. We have a similar situation for the Cooper pair for which any introduction of quantum energy levels in its structure would cause dramatic disagreements with experimental data. Similarly, when the neutron is synthesized in the interior of stars from a proton and an electron, its energy level is unique in the sense that possible excited states do not characterize the neutron any more. The same holds for all hadronic bound states.
It should be stressed that the elimination of the energy spectrum is here referred to solely within the context of hadronic and not quantum mechanics. In fact, a proton and an electron can indeed have an infinite number of excited levels as established by the hydrogen atom. The main point is that all these excited states cause the increase of the mutual distances with consequential elimination of the new hadronic forces and the transition to the full validity of quantum mechanics. In fact, as we shall see in the next chapter, all excited states of the neutron synthesized from a proton and an electron are those of the ordinary hydrogen atom from which the neutron originated. The same occurrence holds for electron bonds in the valence, Cooper and other pairs.
5.5. EXPERIMENTAL VERIFICATION WITH THE BEHAVIOR OF LIGHT
5.5A. The inevitability of the ether as a universal medium
As it is well known in the history of physics, Alhazen initiated in 1021 the conception of light as made up of particles, a conception originated from the capability of light to have momentum, and that was subsequently supported by numerous scientists, most notably by Newton.
The advent in 1873 of Maxwell's equations introduced the alternative conception of light as an electromagnetic wave propagated by a universal substratum, the ether by resolving known insufficiencies of the conception of light as being made up of particles, such a refraction.
In the early part of the 20th century, the admission of a universal substratum caused problematic aspects for the then emerging special relativity, since its basic axiom on the absence of a privileged reference frame was clearly incompatible with the privileged reference frame of the ether. For the specific intent of removing the need of the ether, Einstein introduced in 1905 his celebrated hypothesis that light was made up of photons with energy E = hf (where h is Planck's constant and f the frequency), which hypothesis was supported by the then emerging discovery on the black body radiation. Besides the need to eliminate an absolute reference frame, the photon hypothesis received support from the absence of the so-called ethereal wind, namely, the resistance that Earth and other bodies should experience when moving in space conceived as a medium.
Due to the vast experimental confirmations of the photon hypothesis in atomic spectroscopy, the rest of the 20th century was dominated by the reduction of light to photons with the consequential elimination of the ether as a universal substratum, despite Einstein's own doubts (expressed in some of his letters) on the impossibility of reducing all electromagnetic waves to photons, as it is evidently the case for electromagnetic waves with one meter wavelength, not to mention Einstein's doubts on the final character of quantum mechanics.
During his early studies in the 1950s, Santilli resolved the problem of the "ethereal wind" by reducing all matter to oscillations of the ether (Section 3.2), identified various impossibilities of reducing all electromagnetic waves to photons, recalled the ultimate structure of photons themselves being wavepackets, and restored the Maxwellian conception of electromagnetic waves propagating in the ether as a universal substratum. From the transversal character of the waves, Santilli concludes in his early works of 1952 that the ether is a universal medium of very big rigidity and energy density. As Santilli puts in his early works of 1950s:
You can hear my voice because there is a medium, the atmosphere, propagating sound waves, in which absence sound does not exist. Similarly, you can see my face because of the existence of a universal medium, the ether, creating and propagating light. In the absence of such a medium, light cannot exist, let alone cannot propagate.
The longitudinal character of sound waves (oscillation in the direction of propagation) confirms that the atmosphere is a compressible medium without rigidity. Consequently, the sole possible interpretation of the transversal character of light (oscillations perpendicular to the direction of propagation) is that the ether is a medium with a primary characteristic we call "rigidity." The very big value of the speed of light can solely be represented with the assumption of the ether as a medium with extremely big rigidity and, consequently, very big energy density.
This chapter in general, as well as this section in particular, are devoted to the outline of the vast experimental evidence accumulated since the early 1950s confirming Santilli's original conceptions of the early 1950 according to which:
1) Electromagnetic waves are created and propagated by the ether as a universal medium with very big rigidity and energy density;
2) When electromagnetic waves have a sufficiently small wavelength to allow their meaningful reduction to photons and related interactions with atoms, photons themselves are not "particles," but wavepackets with well defined frequency and wavelength, thus also requiring a universal medium for their very existence and propagation;
3) Electromagnetic waves propagate in vacuum at the speed c, thus verifying the Lorentz-Poincare' symmetry of empty spacetime, and propagate within physical media at the locally varying speed C = c/n, where n is the local index of refraction depending on the frequency of the waves f, density of the medium d, and other local variables, n = n(f, d, ...).
It is hoped that the experimental evidence presented in this chapter establishes that, contrary to political views of having achieved final knowledge on light, following one millennium of studies our knowledge of light is far from being established. It is also hoped that said experimental evidence establishes the need for the interpretation of the ether as a universal substratum characterizing all visible entities in the universe. As Santilli's puts it (see next chapters for details):
The study of the ether as a universal substratum is the ultimate scientific frontier of the third millennium, with potential advances such as longitudinal communications millions of time faster than the speed of transversal waves, spaceships moving at arbitrary speeds without fuel thanks according to geometric locomotions, and other advances beyond our most vivid science fictions of this time.
In this section we review Santilli's studies as summarized in his 1991 monographs (hereon referred to as "Santilli 1991")
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
R. M. Santilli,
Hadronic Press (1991)
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
R. M. Santilli,
Hadronic Press (1991)
Santilli's contributed paper at the 2007 ICDS conference in Bolu, Turkey (hereon referred to as "Santilli 2007"),
Absence of universe expansion, dark matter and dark energy in the new isocosmology with a universal isosymmetry
R. M. Santilli, in the Proceedings of the 2007 ICDS, C. Ozel and V. Cay, Editors, International Academic Press (2008).
and in the recent paper (hereon referred to as "Santilli 2009")
Experimental verification of the isoredshift with expected absence of universe expansion, dark matter and dark energy,
R. M. Santilli, IBR preprint TH-09-35, submitted for publication in July 2009.
5.5B. Experimental verification with light propagating in water.
Since Einstein's proposal of 1905, light propagating within a transparent physical medium, such as water (see Fig. 5.1), has been reduced to photons scattered by the atoms of the medium, or absorbed by the same and then re-emitted. The evident intent or implication is that of rendering special relativity applicable within physical media, since light is reduced to photons propagating in vacuum, with the consequential elimination of the ether as a universal medium.
Despite one century of studies along the latter lines, the reduction of light to photons propagating within physical media remains afflicted by numerous insufficiencies, such as (see Santilli 1991, 2007 and 2009):

Figure 5.18: Light propagating within water constitutes visual experimental confirmation of Santilli's isorelativity due to the impossibility of quantitative representations via the reduction of light to photons scattered among water molecules, and the necessity of the local speed C = c/n as outlined in the text,
1) Fig. 5.18 provides visual evidence of the impossibility of reducing the propagation of light in water to photons scattered among or absorbed by the water molecules, since such a reduction would imply that the great majority of photons must propagate through a very large number of nuclei, as a condition to explain the preservation of the beam. To the authors' best knowledge, only the interpretation of light as a transversal electromagnetic wave propagating within the ether represents the visual evidence of Fig 5.18 because, in this case, the propagation occurs in the universal substratum underlying nuclei.
2) The reduction of light to photons prevents a numerical representation of the (rather large) angle of refraction of light at the water surface. In fact, photons are expected to be scattered or be re-emitted in all directions after hitting the water surface, rather than follow the refractive direction of the beam illustrated in Fig. 5.18. Again, the refraction can be solely represented by the wave interpretation of light with the locally varying speed C = c/n(f, d, ...), where n is the index of refraction (bigger than 1) so familiar prior to Einstein's times.
3) The reduction of light to photons scattered by the water molecules cannot represent the rather large decrease (by about 1/3) of the speed of light in vacuum c when propagating in water, because its numerical representation via photon scatterings would require a virtually complete dispersal of the beam against the visual evidence of Fig, 5.18. A numerical representation via absorption and re-emission of photons is also impossible due to the virtually instantaneous re-emission of absorbed photons. Again, the sole known quantitative representation of the speed of light in water is the historical form C = c/n.
4) The reduction of light to photons is additionally unable to represent experimental evidence on the behavior of electromagnetic waves with large wavelength (such as radio waves with one meter wavelength) when traveling within physical media, since such waves experience the same phenomenology of visible light, yet the reduction of large wavelengths to photons is no longer effective, e.g., due to a dramatic decrease in quantitative predictions via scattering and absorption. Again, the return to the Maxwellian interpretation of light as an electromagnetic wave propagating through the ether is the sole known capable of providing a numerical representation of the local speed of light for all wavelengths. The indication of published evidence to the contrary would be appreciated, with particular reference to the numerical (rather than conceptual) representation of physical evidence via the reduction to photons of electromagnetic waves with large wavelength.
5) The reduction of light to photons traveling in vacuum is finally incompatible with the existence within hyperdense physical media of causal speeds bigger than that of light in vacuum, as expected in the interior of gravitational collapse. At any rate, electromagnetic waves propagating at speeds C = c/n bigger than c, n smaller than 1, have already been identified in laboratory for propagation within special guides reviewed in Section 5.2C, and data elaborations in hadron physics without the aprioristic assumptions of special relativity, systematically show maximal causal speeds within the hyperdense medium inside hadrons as being bigger than that in empty space. In the final analysis, the idea that the maximal causal speed inside a black hole is the same as that in vacuum, has no credibility, let alone no hope for direct experimental verification.
Needless to say, the scattering, as well as absorption followed by re-emission, of photons by the atoms of the medium are beyond doubt, but they can only provide a quantitative representation of the partial dispersal of the light beam within a transparent physical medium with consequential moderate decrease of ist intensity as per visible evidence of Fig. 5.18. Also, Maxwell's wave interpretation of light is not in conflict with its reduction to photons because, as recalled in Section 2.1, photons are not "solid particles," but wavepackets. As such, the reduction of light to photons cannot credibly bypass the fundamental need for the ether allowing the photon wavepackets to exist and propagate.
In summary, due to the impossibility of a numerical representation of all aspects at hand, the above evidence establishes the merely conceptual nature of the reduction to photons of light propagating in water as well as the intent of adapting special relativity to conditions it was not conceived or verified for. The sole quantitative representation known to the authors is that via the Maxwell's conception of light as a transversal electromagnetic wave crated and propagated by a universal substratum, with the consequential local character of the speed of light C = c/n(f, d, ...). The validity of Santilli's isorelativity is then consequential due to its universal symmetry of local speeds of light.
5.5C. Santilli isoredshift
As it is well known, a central prediction of special relativity is the Doppler redshift
where
establishing that, when the source of light moves away from the observer, the frequency of light f is shifted toward the red. This law has been experimentally verified numerous times and confirmed as being exactly valid for the propagation of light in vacuum, a feature tacitly assumed hereon.
Despite these successes, the Doppler redshift has no experimental verification at all for for the propagation of light within transparent physical media. In this case, light is generally reduced to photons scattering among or absorbed by the molecules of the medium. Law (5.116) is then recovered from the fact that photons propagate in vacuum.
Santilli's studies have provided a dramatic revision of the latter beliefs. First of all, Santilli (1991) has established the need for the return to the interpretation of light as electromagnetic waves propagating within a universal substratum. Secondly, Santilli has re-established the speed of light as the local variable C = c/n used for centuries prior to Einstein. Thirdly, Santilli has proved that, when the speed of light within a physical medium is no longer c, the universal Lorentz-Poincare'-Santilli isosymmetry for all possible local speeds C = c/n characterizes the Doppler-Santilli isoredshift reviewed in Section 3.10G, Eq. (3.98)
where n4 is the local index of refraction, and n3 is the space characteristic quantity of the medium in the direction of propagation of light.
The above isolaw establishes that, since n4 is bigger than n3 (for all media of moderate density such as air or water), when the light source moves away from the observer and light propagates within a physical medium, there is a redshift bigger than that predicted by special relativity. The above law was then confirmed in astrophysics by Mignani in 1992 and in other fields as reviewed in the next section.
At the ICDS conference in Bolu, Turkey, of 2007, Santilli pointed out that isoredshift (5.118) admits no divergent value for v = c and, similarly, it does not admit a null shift for v = 0 because the space characteristic quantity n3 generally depends on the speed, energy and other quantities. In this way, Santilli formulated the isotopic redshift for null speeds
today known as Santilli isoredshift and referred to a shift toward the red of the frequency of light propagating within a transparent physical medium without any relative motion among the source, the medium and the observer.
Santilli's argument is that, when propagating within a physical medium, light loses energy E = hf to the medium due to interactions, with consequential decrease of the frequency f. Alternatively, the geometric interpretation is that a physical medium, whether characterized by matter or light, causes the mutation of the Minkowski spacetime of the vacuum with consequential decrease of its speed and resulting decrease of the frequency.
In his 2007 paper [loc. cit.], Santilli discusses in details the structural differences between his isoredshift and the numerous proposals intended to eliminate the expansion of the universe known as tired light. In fact, all the latter hypotheses assume the reduction of light to photons propagating in vacuum at the speed c, while Santilli isoredshift is based on a structural change of spacetime with alteration of the speed of light caused by intergalactic physical medium (see next section). Santilli 2007 paper ends with the proposal of three easily feasible experiments for the verification of the denial of his isoredshift.
5.5D. Experimental confirmation of Santilli isoredshift
In his recent paper of 2009, Santilli reported preliminary confirmations of the isoredshift via the following realization of Experiment 10.2, page 237, Santilli 2007. For this scope, Santilli built a schedule 80, high pressure, carbon steel pipe 60' = 28.3 m long, 5" = 12.7 cm in outside diameter, and transparent ends with 2" = 5.6~ cm thick lexan. The pipe was filled up with filtered air at 2,000 psi = 138 bar pressure. A monochromatic blue light with wavelength 473 nm from a 100 mW diode laser was passed through the pipe and its wavelength measured in air following said passage, with and accuracy to a fraction of a nm.
.
The compressed air inside the pipe was discharged by restoring atmospheric pressure, but keeping the two lexan terminals. The same monochromatic blue light was then passed through the pipe at atmospheric pressure and its wavelength measured also in air after passing through the pipe with the same experimental set up used at pressure and without any alteration.

Figure 5.19: A view of the Isoredshift Testing Station built by Santilli in June 2009 at the laboratory of the Institute for Basic Research in Florida. Additional pictures are available from the websiteIsoredshift Testing Station R. Anderson, The R. M. Santilli Foundation.
A comparison of the data shows a clear increase over background/or statistical fluctuations of the wavelength of light λ2 passing through the pipe at 2,000 psi = 138 bar compared to the wavelength λ1 at atmospheric pressure. In particular, as shown in Figs. 6 and 5.20, the measurements showed a redshift characterized by the deviation of the blue laser light well over background of about 0.5 nm,
when propagating through the indicated pipe plus the lexan terminals, compared to the same travel of the same light in air plus the travel through the two lexan terminals. Since the deviation occurs without any relative movement of the laser source, the medium or the detector, the above measurements confirm Santilli isoredshift. By assuming that the speed of light in air is the same as that in vacuum, the corresponding frequencies f2 and f1 are related to the wavelength by the known law
Therefore, the increase of the wavelength implies the decrease of the frequency, thus confirming Santilli isoredshift. Needless to say, the above measurements should be considered preliminary and in need of various reruns and improvements currently under way (October 2009). Nevertheless, isoredshift (5.121) has been released in view of: the consistency of the results; its compatibility with other propagations of light within physical media; as well as a number of unverified indications of similar isoredshifts all recommended for test, such as radio communications received on Earth from spaceships when passing in the back of planetary atmospheres, light propagating through long optical fibers, and other cases. All this information eliminates vacuous, not so unfrequent theoretical disproofs of measurements, by confirming that experimental measurements can be credibly dismissed solely with counter-measurements.
Figure 5.20: A view of the first detection of Santilli's isoredshift obtained in June 27, 2009, at the Isoredshift Testing Station of the preceding figure showing a clear increase of the wavelength with consequential clear decrease of the frequency of the used blue laser light. Additional pictures and data are available from the website Inconsistencies of special relativity within physical media R. Anderson, The R.M. Santilli Foundation.
5.5E. Experimental verification with the colors our atmosphere
The insufficiencies of the reduction of light to photons identified in the preceding section persist for all propagations within transparent physical media, not only on Earth, but also in astrophysics and cosmology (see next section).
As an additional example for conditions on Earth, consider the propagation of light in our atmosphere. Visual evidence establishes that, when the Sun is at the Zenith, our atmosphere is predominantly blue not only toward the Zenith, but also toward the horizon, while the atmosphere at Sunset and Sunrise is predominantly red (Fig. 5.19).
The interpretation of the above evidence assumed during the past century has been that the blue color of the sky is due to the scattering of (a small portion of the Sun) blue light, since red light is absorbed by the atmosphere. For Sunset and Sunrise the conventional interpretation is that we have the opposite occurrence, namely, we have the absorption of all light frequencies except for the frequencies of red light.

Figure 5.21: Views taken by the author in Palm Harbor, Florida, of our horizon when the Sun is at the Zenith (left), at Sunset (top right) and Sunrise (bottom right), illustrating the predominant blue color when the Sun is at the Zenith and the predominant red color at both Sunset and Sunrise. Comprehensive color pictures are available in the website Inconsistencies of special relativity within physical media
R. Anderson.
In Santilli's view, the interpretation of the blue color of the sky is correct and confirmed by experimental evidence of light propagating within other transparent physical media. For instance, the color of sea water becomes progressively blue with the increase of the depth, to the point that at about 20 m depth only the blue light remains visible, while all other colors are absorbed by the medium. In any case, the conventional quantum scattering theory confirms that the penetration of photons within a transparent medium is proportional to the frequency, the harder the photons, the deeper being the penetration. Alternatively, quantum scattering theory establishes beyond doubt that red light is absorbed by media much more than blue light.
By contrast, the current interpretation of the predominant red color at Sunset and Sunrise is in disagreement with various physical laws, being a mere consequence of the adaptation of physical reality to special relativity without prior independent experimental verifications.
Let us recall that Earth perimeter (at the Equator) is of about 40,000 km. Hence, at Sunset we have the tangential speed away from the Sun
By recalling the conventional Doppler shift law for the frequency terminated at the first term in the expansion in terms of v/c
tangential speed (5.1) causes a conventional Doppler redshift with value
that, being very small, is basically unable to represent the transition of the color of the sky at the horizon from blue during the day to red at Sunset (Fig. 5.19).
Figure 5.22: A schematic views by Santilli to illustrate the conventional Doppler redshift at Sunset and the conventional blueshift at Sunrise, as discussed in the text.
For the case of Sunrise, we move toward the Sun at speed (5.124), in which case we have the conventional Doppler blueshift
with value
that, besides being also very small, its sign is in violation of visual evidence at the horizon of red rather than blue.
In summary, the strict application of special relativity to light requires that Sunset should be red and Sunrise should be blue. By contrast, visual evidence establishes that this is not the case, because both Sunset and Sunrise are predominantly red, thus establishing the presence of physical conditions beyond those of the exact validity of special relativity in favor of Santilli's covering isorelativity as shown in the next section.
Assuming that with the introduction of unknown ad hoc parameters or functions, the above physical evidence for the behavior of light at Sunset and Sunrise is manipulated to verify special relativity, we still remain with the basic inability by special relativity to represent quantitatively the transition of the color of the horizon from blue to red at both Sunset and Sunrise, as shown in Fig. 5.21. Therefore, we reach the same conclusion as that of Section 5.5B, namely, that special relativity is inapplicable within physical media at large, whether gas or liquid (rather large departures for solids or hyperdense media are discussed below).
In his 2009 paper, Santilli has shown that isoredshift (5.121) provides a numerical representation of the color of our atmosphere at the Sunset and Sunrise, the blue color for the Sun at the Zenith being due to known absorption of the other colors. This numerical interpretation evidently provides significant support to the existence of Santilli isoredshift.
The color of our atmosphere is a very complex event because resulting from a number of different processes, such as:
a) The scattering of photons among the atoms of our atmosphere that is proportional to the frequency, as established by the relativistic quantum scattering theory;
b) The absorption of light by our atmosphere that is inversely proportional to the frequency, as established by the propagation of light within various transparent media, such as sea water;
c) The Doppler redshift occurring at Sunset, Eq. (5.125);
d) The Doppler blueshift occurring at Sunrise, Eq. (5.127); and
e) Santilli isoredshift that is proportional to the density of the transparent medium (as well dependent on other characteristics not essential for the problem at hand).
As shown in Section 3, the sole use of processes a) to d) does not alow a quantitative representation of all colors of our atmosphere. By contrast, the addition of isoredshift e) does indeed allow the first quantitative representation known to this author.
Again, processes a) and b) do represent quantitatively the blue color of our atmosphere when the Sun is at the Zenith, including the color of the horizon, under the absorption of all colors with bigger wavelengths, in accordance with quantum scattering theory.
When passing to Sunset and Sunrise, we should equally assume that solely the blue light penetrates deep into the atmosphere and other colors are absorbed. In any case, if the red color is absorbed by our atmosphere when the Sun is at the Zenith, the same absorption becomes mandatory for a serious study when dealing with the much longer propagation of light at the horizon.
In this way, the problem of the color at Sunset and Sunrise is reduced to a quantitative study of the transition of blue to red light in both cases. The opposing contributions of Doppler's redshift at Sunset and blueshift at Sunrise are given by the measurable difference in red color between Sunset and Sunrise that is not addressed in this paper, but hoped it is measured by experimentalists in the field.
The blue light of the sky we are referring to has the wavelength of 470 nm, while the red light we see at Sunset and Sunrise has the wavelength of about 670 nm. Therefore, at Sunset and Sunrise we have the isoredshift
Measurement (5.122) shows a deviation of 0.5 nm for blue light traveling for 60' = 28.3 m in air at 2000 psi = 138 bar. Assuming a linear proportionality of the isoredshift on length, a travel for 28.3 m at 138 bar is equivalent to the travel at 1~ bar of
Consequently, the needed isoredshift of 200 nm can be accounted for by the proportion
namely, measurement (5.122) predicts that blue light is shifted into red light when propagating for 1,562 Km in atmosphere assumed at 1 ~bar.
However, Earth is curved and Sun light at Sunset and Sunrise passes from empty space to 1 bar approximately in 6,000 Km according to a law that, in first approximation, can be assumed as being inversely proportional to the square elevation from sea level. Consequently, 1,562 Km are indeed a good approximation of the 6,000 Km travel of light from empty space to 1~ bar.
This confirms that Santilli isoredshift does indeed provide a quantitative representation of the predominance of red at Sunset and Sunrise. It should be noted that the full treatment of the colors at Sunset and Sunrise requires the Doppler-Santilli isoshift. This approach has not been considered in this paper due to the small value of the Doppler redshift (5.126) at Sunset and blue shift (5.128) at Sunrise, but it is hoped will be treated in a future paper.
5.6. EXPERIMENTAL VERIFICATIONS IN ASTROPHYSICS
5.6A. The unreassuring condition of 20th century astrophysics
One of the biggest controversies in the history of science has been the interpretation of the cosmological redshift via the "big bang" theory. This unreassuring condition has been aggravated more recently by additional controversies on far reaching conjectures, such as those of "dark matter" and "dark energy."
Having been a former insider in high ranking academia, Santilli has repeatedly stated in his writings that all these conjectures have been proposed for the specific purpose of extending the applicability of Einsteinian theories well beyond the conditions of their conception and experimental verification, and that, to maintain their validity, said conjectures are collegially preferred over the more plausible possibility of deviations from special relativity under conditions beyond those of its original conception and experimental verification.
In fact, the "big bang" conjecture was specifically conceived and developed to adapt the expansion of the universe to a basic axiom of special relativity, Doppler's redshift, despite the following inconsistencies pointed out by Santilli various times and expected to be known by experts to qualify as such:
A) Since the primordial explosion is assumed as being occurred about 15 billion years ago and occurred at one point in space, said explosion should have created a very large area in the universe without any galaxy at all, an occurrence disproved by astrophysical evidence on the distribution of galaxies throughout the universe;
B) Since the speed of galaxies is assumed to be proportional to the distance from Earth and be the same in all directions from Earth, the "big bang" conjecture causes a return to the middle age conception of Earth at the center of the universe, with the "big bang" occurred in its galactic environment, while alternative popular views (such as the "rubber band" model and the like) are excluded by the occurrence of the primordial explosion at one point in space with consequential necessary anisotropy;
C) The "big bang" conjecture is ultimately in conflict with gravitation because the expansion of the universe should decrease over 15 billions years due to gravitational attraction, rather than increase with the distance as per experimental data on cosmological redshifts; and other rather serious inconsistencies identified in the technical literature.
Similarly, it is known that "dark matter" is also a consequence of an additional adaptation of the dynamics of galaxies to special relativity. In fact, Santilli has shown that "dark matter" is a consequence of the assumption within the dense gas filling up the interior of galaxies of the speed of light c in vacuum, contrary to the evidence indicated in the preceding sections.
The conjecture of "dark matter" assumes unreassuring character when one meditates a moment on Santilli's comment that, if uniformly distributed, "dark matter" cannot possibly have any measurable effects on the dynamics of stars. Consequently, "dark matter" must be placed ahead or behind a start to have its trajectory comply with the predictions of special relativity, but then the trajectory of a near-by star is outside these preferred prediction.
Similarly, Santilli has stressed that "dark energy" is yet an additional adaptation of physical evidence to special relativity, again, without any prior independent experimental backing. More specifically, Santilli has shown that "dark energy" is a consequence of the assumption of the speed of light in vacuum as the maximal causal speed in the interior} of stars, quasars and black holes.
More specifically, Santilli has shown that the conjecture of "dark energy" is a consequence of the (generally tacit) assumption of the validity of Einstein's equivalence law E = mc2 for all possible conditions existing in the universe. The unreassuring condition is created by the fact that Einstein formulated his equivalence law, specifically, for point-like particles. Therefore, the applicability of the same equivalence law for the energy equivalence of stars, quasars and black holes is purely hypothetical.
It is then hoped the serious scholar will admit that astrophysics and cosmology cannot remain quantitative sciences without a joint study of ongoing far reaching conjectures based on the validity of special relativity everywhere throughout the universe as well as of deviations from special relativity for conditions beyond those originally conceived by Einstein.
In this section we shall review Santilli's studies establishing the absence of the universe expansion, "dark matter" and "dark energy," while jointly providing a rather momentous verification of the covering Santilli isorelativity.
In this section we review the same original references of the preceding section, namely, Santilli's studies as summarized in his 1991 monographs (hereon referred to as "Santilli 1991")
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
R. M. Santilli,
Hadronic Press (1991)
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
R. M. Santilli,
Hadronic Press (1991)
Santilli's contributed paper at the 2007 ICDS conference in Bolu, Turkey (hereon referred to as "Santilli 2007"),
Absence of universe expansion, dark matter and dark energy in the new isocosmology with a universal isosymmetry
R. M. Santilli, in the Proceedings of the 2007 ICDS, C. Ozel and V. Cay, Editors, International Academic Press (2008).
and in the recent paper (hereon referred to as "Santilli 2009")
Experimental verification of the isoredshift with expected absence of universe expansion, dark matter and dark energy,
R. M. Santilli, IBR preprint TH-09-35, submitted for publication in July 2009.
5.6B. Absence of universe expansion
Recall that the cosmological redshift z is defined by
and it has been interpreted throughout the 20th century as being due to the Doppler shiftcosm
where v is the expansion speed with respect to Earth, thus yielding the well known expression
Santilli (1991, 2007, 2009) has pointed out that space can be considered as being empty only at short distances in astronomical scale, such as for interplanetary distances, while space is indeed a physical medium at intergalactic distances. In fact, the entire universe can be observed from any of its points. Hence, each point of intergalactic space is traversed by light originating from all of the universe, thus characterizing a local energy density d different than zero. Additionally, space is full of cosmic rays, hydrogen and matter that, again at intergalactic distances, contribute to space as being a physical medium with cosmological speed of light and index of refraction derived from the experimental evidence of Section 5.5

Figure 5.22: Santilli's innovative conception of intergalactic space is that of a medium with high energy density primarily characterized by light, with minor contributions from cosmic rays, hydrogen and dust. He argues that we can see the entire universe from any point in intergalactic space, thus implying that every point is crosses by light originating from the entire universe. Santilli has then eliminated the expansion of the universe by showing theoretically and experimentally (Section 5.5) that light propagating within a physical medium, in this case "light propagating through light," experience a redshift without any relative motion. Rather than adapting nature to a preferred theory, Santilli has adapted the theory to experimental evidence, by resolving in this way controversies of historical proportions.
The admission of the local character of the speed of light eliminates any need for the expansion of the universe. In fact, Santilli (2007) first assumes the limit case of no intergalactic motion at all,
As a result, the cosmological redshift cannot any longer be interpreted as due to the Doppler's shift. However, by recalling the expression λ f = C, it is easy to see that the cosmological redshift can be numerically represented via the new law known as Santilli cosmological isoredshift
referred to a redshift of light not due to relative motion, but to the loss of energy to the medium due to interactions, with consequential decrease of the frequency.
As the reader knows, the prefix "iso" originating from Santilli's novel underlying mathematics and relativity known as isotopies in the Greek meaning of preserving the original axioms. As Santilli puts it: Rather than abusing Einstein's name for personal gains, my way of honoring Einstein is by showing that his axioms admit a broader realization dramatically extending their original conditions of applicability.
Needless to say, the above cosmological isoredshift does not exclude small local expansions or contractions of the universe, as it is expected to be the case for the gravitational repulsion between matter and antimatter galaxies, and for the gravitational attraction between matter galaxies, respectively. However, expansions and contractions should be of such a minimal value and anisotropic character not implying the Middle Age belief that Earth is at the center of the universe.
It is evident that Santilli cosmological isoredshift implies the expansion of the universe as well as the increase of the expansion with the distance. To have an explicit illustration, Santilli introduces as a working assumption a simple functional dependence of the cosmological index of refraction of the type
where N is a positive constant, under which cosmological isoredshift becomes
thus verifying Hubble's law for wavelengths essentially assumed as constant. We then have the following structure model of Hubble's constant
Additionally, the model produces a dependence of the cosmological isoredshift on the frequency, wavelength, distance, energy density, temperature, and other characteristics.
Note that similar results can be obtained via Santilli isoredshift defined according to law (5.120). To understand the complexity of the model, one should keep in mind that, from the law c = λ f, the speed of light can decrease because of :1) The decrease of the frequency only; 2) the decrease of the wavelength only; and 3) The decrease of both the frequency and the wavelength. Santilli's cosmological isoredshift is based in the latter case.
Finally, Santilli points out that the "big bang" conjecture does not provide a plausible explanation of the background radiation because of controversies in its emission, as well as the fact that, following some 15 billions years, the radiation emitted by the presumed primordial explosion can be proved to have been absorbed by galaxies.
By contrast, Santilli cosmological isoredshift provides a quantitative representation of the background radiation. In fact, a decrease of the frequency requires the necessary decrease of the energy of light.
In his 2007 paper, Santilli presents a detailed differentiation between his interpretation of the cosmological redshift and the numerous alternative interpretations known under the name of "tired light." A main differentiation is that the former is based on a structural lifting of special relativity, while the latter are based on special relativity and the reduction of light to photons traveling at the speed c. An additional interpretation is the admission in the former of a locally varying speed of light that is generally absent in the latter. A further difference is Santilli's innovative conception of intergalactic space as a medium characterized by light, while the notion of a medium is generally absent in "tired light" models.
5.6C. Absence of "dark matter"
The hypothesis of "dark matter" originated from an anomalous behavior of peripheral stars in a galaxy as compared to stars in its interior. But the only means for measurements of far away stars available on Earth is light. Therefore, said anomaly is, again, derived from anomalous differences between the redshift of exterior and interior stars in a given galaxy.
thus yielding a numerical representation of the continuous presence through times of the same background radiation since space cannot possibly absorb it.

Figure 5.23. The 20th century astrophysics and cosmology assumed that interstellar space inside a given galaxy is empty so as to verify special relativity. Santilli (2007) pointed out that space within a galaxy is filled up with matter whose density decreases with the radial distance from the galactic center, thus causing a slowdown of the speed of light that decreases with the increase of said distance, by eliminating altogether the need for dark matter.
Santilli (2007) pointed out that space within a given galaxy is indeed a physical medium, actually with much bigger energy density than intergalactic space. Therefore, the cosmological isoredshift applies for stars belonging to a galaxy, and he writes
with galactic isoredshift for the case of stars having null radial speed with respect to Earth (e.g., as in Figure 5.22)
The plot of the anomalous behavior of stars can be achieved via a plot of galactic index of refraction since it clearly varies with the distance from the galactic center.
It should be noted that stars belonging to a galaxy may have speeds toward and away from Earth. Additionally, galaxies and their interior media are highly anisotropic. Consequently, the general case of galactic dynamics requires specific studies per each galaxy and belongs to the field of Doppler-Santilli isoredshift, namely, a redshift due to a combination of a conventional redshift caused by relative motion and a complex isoredshift caused by physical media with locally varying densities.
5.6D. Absence of "dark energy"
Yet another reason for uneasiness in the astrophysics and cosmology of the 20th century is the rather widespread assumption of the validity of Einstein's equivalence principle
throughout the universe, expectedly, until the end of time, without any scrutiny, thus adapting the universe to a preferred theory.
Needless to say, the equivalence principle is indeed valid for the conditions of its original conception and experimental verification, point-like particles moving in vacuum, such as particles in accelerators. However, the assumption of the same principle without any experimental evidence for extended bodies becomes a theology in Santilli's view. Point particles have no dimension. Consequently, their maximal causal speed is the speed of light in vacuum c.
Consequently, the assumption of special relativity implies the abstraction of the universe, including all its stars, quasars and black holes, to a set of isolated massive points, with consequential universality of the speed of light and insufficient energy to explain its dynamics.
At this point the need for an invariant, universal, covering relativity becomes crucial to prevent endless trials and errors. Recall from Section 3.10 the direct universality of Santilli's isorelativity and the experimental evidence in particle physics, nuclear physics, astrophysics and other fields outlined in this chapter according to which the maximal causal speed within hyperdense matter (such as in the interior of hadrons, nuclei and stars) is bigger than the speed of light in vacuum, with consequential bigger values of the energy equivalence.
Recall also that the covering Lorentz-Poincare'-Santilli isosymmetry characterizes the light isocone (the light cone on Minkowski-Santilli isospace over the isofield, e.g., in the (3, 4)-space
from which we have Santilli maximal causal speed, Eq. (3.95), i.e.,
Dark energy is then eliminated by merely noting that the average maximal causal speed of the universe, including the interior} of stars, quasars and black holes, is expected as being much bigger than the speed of light in vacuum. As an illustration, the plot of experimental data on the structure of the neutron and the proton-antiproton fireball of the Bose-Einstein correlation yields the value Vmax = 1.653 c (Section 5.2). By recalling that black holes have a dramatically bigger density than that of the neutron or the proton-antiproton fireball, values much bigger than 1.653 c are expected in the universe.

Figure 5.24. Santilli (2007) has shown that the current belief on "dark energy," is a consequence of the belief that the speed of light c is a "universal constant," thus being also valid in the interior of black holes depicted in this figure. The paradoxical character of these beliefs is that the lack of validity in the interior of gravitational collapse of conventional laws of physics is widely accepted in academia, thus eliminating the plausibility that the maximal causal speed in the interior of stars, quasars and black holes is the speed of light in vacuum. The admission of maximal causal speeds in the hyperdense interior of astrophysical bodies bigger than the speed of light in vacuum completely eliminates the conjectural belief of "dark energy," as reviewed in the text.
To provide an initial but quantitative representation, by assuming ns as the average of the three space characteristic quantities, the total energy of the universe is given by
The assumption of Santilli's covering isorelativity allows an exact representation of the needed energy, the excess originating from the maximal causal speed in the interior of astrophysical bodies being bigger than c. In this case, Santilli writes the expression
The current estimate of the value of the dark energy can be used to provide an estimate of the average value of Vmax, average for the universe. For instance, assuming at the limit that the missing energy is 100-times the Einsteinian value, we get the estimate
which is a rather reasonable value if one takes into account its limit character (100% excess energy), and the increasing number of black holes in the universe.
In short, rather than adapting the universe to verify a preferred theory, "dark energy" is a direct experimental evidence of the deviations of the universe from special relativity, with particular reference to deviations from the universal character of the speed of light in vacuum as the maximal causal speed in favor of much bigger average values.
5.6E. Experimental verification with quasar redshifts
As it is well known, Halton Arp, a member of the Astrophysics Department of Harvard University, provided in 1987, see for instance the monograph
Quasars Redshifts and Controversies, H. Arp, Interstellar media, Berkeley (1987)
experimental evidence that certain quasars are at rest with respect to their associated galaxies, even though their cosmological redshifts are dramatically different. Since such a view is at clear violation of Einsteinian doctrines, Arp experienced extreme academic obstructions, including the termination of his academic position at Harvard by his colleagues.
In 1989, J. Sulentic, see, e.g., the paper
J. W. Sulentic, Astrophys. J. Vol. 343, 54 (1989).
provided major astrophysical evidence of the correctness of Arp's view via gamma spectroscopy proving the existence of an actual physical contact between certain quasars and their associated galaxies, despite dramatic differences in their cosmological redshifts. The occurrence was more recently confirmed by other observations and it is now an astrophysical reality.
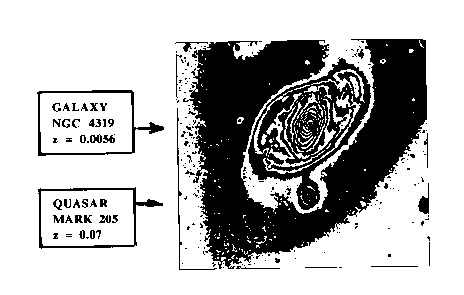
Figure 5.24: An example of clear astrophysical evidence beyond the capabilities of special relativity: the physical connection between the galaxy NGC 4319 and the quasar Mark 205 obtained by gamma spectroscopy, while their cosmological redshift of the galaxy is z = 0.07 and that of the galaxy is z = 0.0056. Any plausible interpretation of this difference requires a departures from special relativity, since the latter implies that physically connected astrophysical bodies must have the same speed. Santilli isoredshift provides a numerical representation of the above dramatically different cosmological redshifts, as outlined in the text.
The following memoirs of 1988
R. M. Santilli, Hadronic J. Suppl. Vol. 4A, issues 1, 2, 3, 4 (1988).
(see also Santilli 1991 for an update) proposed the isotopic interpretation of Arp-Sulentic data via isorelativity and iso-Minkowskian geometry. Santilli's main hypothesis was simply that light exits the huge quasars chromospheres already redshifted due to the internal decrease of its speed c, according to the Doppler-Santilli isolaw invariant under the Lorentz-Santilli isosymmetry
We are here dealing with an experimental verification beyond credible doubt of the local character of the speed of light, Santilli isoredshift of the preceding section, and Santilli isorelativity at large outlined in Section 3.10. According to special relativity, when a quasar and a galaxy are physically associated, they must have the same cosmological redshift. The clear experimental evidence that they have instead dramatically different redshifts is prove beyond credible doubt of deviations from special relativity in favor of a covering relativity.
Santilli's isorelativity provides a numerical representation of the indicated cosmological redshift. In essence, quasars have huge chromospheres at times as big an an entire galaxy. By contrast, galaxies have a relatively much more modest intergalactic gases. Therefore, the dramatically different cosmological redshifts establishes that quasar light has been primarily redshifted during its travel within the quasar chromosphere. By comparison, light has been minimally redshifted by the medium inside the galaxy. In this way, the light from the quasar and its associated galaxy reaches empty space dramatically redshifted to initiate their long intergalactic travel toward Earth.
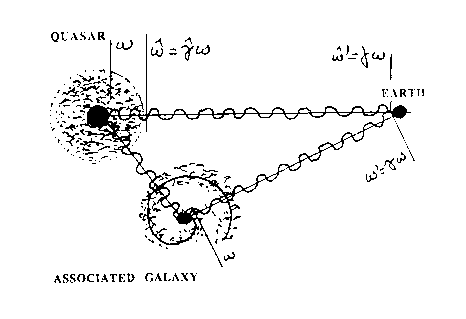
Figure 5.26: A reproduction of the original drawing by Santilli of 1988 illustrating the hypothesis on the isotopic origin of the quasar redshift, that is, a redshift due to the geometry of the huge quasars chromosphere. According to isorelativity, a first major component on the cosmological redshift of quasars is due to the decrease of the speed of light in its chromospheres. A second contribution is due to the anisotropy of the same medium. These two contributions then account for the complete difference in cosmological redshift between the quasars and the associated galaxy under the same relative speed v with respect to Earth.
In the 1992 paper
Quasar redshift in iso-Minkowski space
R. Mignani,
Physics Essays Vol. 5, 531-535 (1992)
Mignani provided a direct experimental verification of the Doppler-Santilli isoredshift for the case of quasars that are associated to a galaxy according to clear gamma spectroscopy, yet the quasar and associated galaxy have a dramatically different cosmological redshift.
In essence, Mignani elaborated several data by Arp via the following relation for the cosmological redshift derived from the Doppler-Santilli isolaw (5.152)
(5.153)
bs [(Df + 1)2-1]x[(Df'+1)2-1]
-- = ----------------------------------- = B,
b4 [(Df + 1)2+1]x[(Df'+1)2+1]
where Df' represents the isotopic redshift for the quasar and Df represents the measured conventional redshift for the associated galaxy.
The above values provide a clear confirmation of Santilli isorelativity and underlying isogeometrization of physical media. In fact, the data show that all values B = (bs / b4) are positive and bigger than one, exactly as predicted.
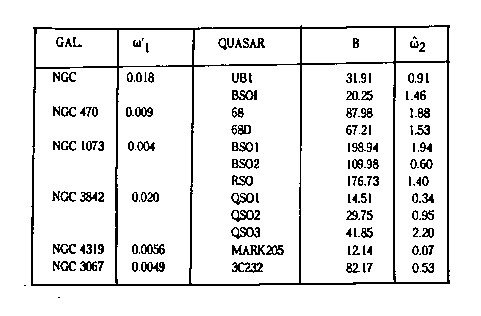
Figure 5.27: The 1992 data by Mignani following Santilli 1988 hypothesis on the isotopic origin of quasar's cosmological redshift that provide a numerical, exact and invariant representation of the difference in cosmological redshifts between numerous quasars and their associates galaxies.
The identification of the individual values bs and b4 requires at least one additional experimental measurement, such as the average speed of light c C = cb4 = c/n4 in the quasar chromospheres. Such a value would fix b4. Then, bs could be computed from the B-ratios. As an indication, the assumption for quasar UB1 of the average speed of light in its chromosphere c = 0.80 x c0 would yield the value bs = 40.
It should be noted that Mignani's calculations are based on the assumption of the expansion of the universe, and consequential conventional interpretation of the conventional Doppler's shift for light in vacuum. Following the experimental confirmation of Santilli's isoredshift outlined in the preceding section, Mignani's calculations should be revised for the complete reduction of the cosmological redshift to quasars and associated galaxies essentially at rest with respect to Earth in accordance with Section 5.6B.
In addition to the difference in cosmological redshifts between quasars and their associated galaxies when physically connected, quasars possess an internal redshift and blueshift that is a typical manifestation of the dependence of the index of refraction on its frequency,
The most plausible exact interpretation of the internal quasar redshifts and blueshifts known to the authors is that permitted by isorelativity and presented in the paper
R. M. Santilli, contributed paper in Frontiers of Fundamental Physics, F. Selleri and M. Barone, Editors, Editors, Plenum, New York (1994).
via a dependence of the local index of refraction from the frequency of light of the type
that provides an exact and invariant fit of Sulentic's experimental data.
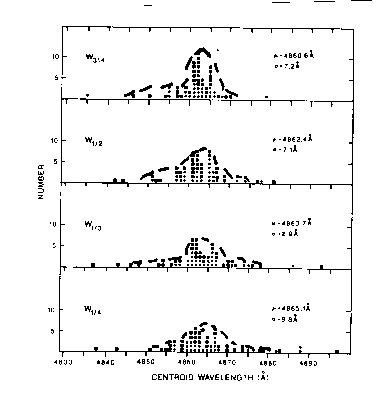
Figure 28: The numerical, exact and invariant fit of the experimental data by Sulentic on the quasars internal blue- and red-shifts done by Santilli via the use of isorelativity. The above interpretation is prohibited by the validity of special relativity within physical media, because the "universal constancy of the speed of light" prohibits a frequency dependence that is specific for locally varying speeds. in different words, isorelativity essentially reduces the quasars internal red- and blue-shifts to Newton spectral decomposition of light.
In summary, according to Santilli's isorelativity, quasar cosmological redshifts and their internal red- and blue-shifts are due to interior physical characteristics of the quasars chromospheres and, more specifically, to their inhomogeneity and anisotropy, that is, to the departures from (rather than verification of) the geometry of empty space occurring within physical media. The understanding is that the fit of Figure 30 can ultimately result to be due to the contributions from the isoblueshift in the hyperdense interior of quasars, the isoredshift in the quasar chromosphere, and the isoredshift in intergalatic media.
5.7. EXPERIMENTAL VERIFICATION WITH ANTIMATTER AND COSMOLOGY
5.7A. The unreassuring condition of 20th century antimatter and cosmology
As indicated in Chapter 1, antimatter caused one of the biggest scientific imbalances of the 20th century due to the lack of any classical treatment of antimatter, as a result of which matter was treated at all levels of study, from Newton to second quantization, while antimatter was solely studied at the level of second quantization.
This historical imbalance impacted in particular 20th century cosmology since the universe was widely assumed as being solely composed of matter.
However, Santilli points out that evidence on the existence in the universe of antimatter stars is available on Earth. For instance, Santilli indicates that the 1927 Tunguska explosions in Siberia can solely be explained scientifically, that is, quantitatively, as being caused by an antimatter asteroid, due to the complete absence of any debris compared to the vastity of the devastation on the ground. In fact, matter asteroid leave an impact crater on the ground while it is impossible for them to evaporate completely.
Similarly, it is at times indicated that antimatter cosmic rays do not exist because they have not been detected on Earth. However, Santilli points out that only matter cosmic rays can reach Earth's surface since all antimatter cosmic rays must annihilate in the upper region of our atmosphere. In fact, astronauts and cosmonauts indicate to have seen "flashes" of light in the upper atmosphere when in darkness.
Independently from all the above, a plausible act of creation of the universe would require a joint creation of matter and antimatter, e.g., in the event creation originated from energy. These and numerous additional aspects motivated Santilli to initiate a serious experimental study of antimatter at all levels.
5.7B. Experimental verification of Santilli's isodual theory of antimatter
As outlined in Chapter 3, Santilli has resolved the historical imbalance on antimatter by achieving the new isodual theory that permits the study of antimatter at all levels, from classical to operator mechanics, by restoring in this way a full democracy of study between matter and antimatter.
It is important for completeness to recall from Chapter 3 that Santilli's isodual theory of antimatter verifies all known experimental data on antimatter, because the Newton-Santilli isodual equations are anti-isomorphic to the conventional equations as requested by physical evidence, and the isodual map is equivalent to charge conjugation at the operator level.
These important discoveries have created the previously missing antimatter astrophysics and cosmology whose scope is that of searching for antimatter stars, quasars and galaxies via the predicted repulsion of isodual photons by matter gravitational fields, and the study of similar predicted events. For more details, we refer the reader to Santilli's monograph
"Isodual Theory of Antimatter, with Applications to Antigravity, Grand Unification and Cosmology,"
5.7C. Santilli's isoselfdual cosmologies.
Santilli's studies in cosmologies are the most difficult to understand on technical grounds because, in line his definition of "cosmology," they include all preceding advances. Therefore, the technical understanding on this section requires the knowledge of the all five volumes of HMMC,
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V:
Partial presentations can be found in the papers
Isominkowskian formulation of gravitation and cosmology
Absence of universe expansion, dark matter and dark energy in the new isocosmology with a universal isosymmetry
R. M. Santilli,
Springer (2006)
R. M. Santilli, International Academic Press (2008)
R. M. Santilli,
in the proceedings of "Modern modified Theories of Gravitation and Cosmology," israel, 1996, E. I. Guendelman, Editor, Hadronic Press, pages 113-165(1998)
R. M. Santilli, in the Proceedings of the 2007 ICDS, C. Ozel and V. Cay, Editors, International Academic Press (2008).

FIGURE 26: Santilli has defined "distressing" his studies of 20th century cosmology because of excessive assumptions, such as the expansion of the universe, "dark matter" and "dark energy," intended to maintain the validity of Einsteinian theories under conditions they were not conceived, tested or intended for, rather than admitting their limitations, as well as the exclusion in cosmological models of biological structure and antimatter against the very Greek meaning of the word "cosmos."
An effective way to outline Santilli's cosmological studies is via the following statement he released for this volume:
The study of mathematics, physics and chemistry has been for me reason of great intellectual excitement in seeing simply magnificent constructions of the human mind, combined with great distress in seeing their misuse for conditions they were not intended for.
The first reason for intellectual excitement has been for me the majestic axiomatic structure of special relativity and its impressive experimental verifications for the conditions of its original conception (point-particles and electromagnetic waves propagating in vacuum), combined with great distress in seeing the application of the same theory under conditions vastly beyond those of its original conception without any serious scrutiny on evident limitations of the formalism, such as its local-differential character that limits the applicability to a finite set of isolated points.
Another reason for intellectual excitement has been for me the equally majestic axiomatic structure of quantum mechanics as well as its impressive experimental verifications for the same conditions recalled above, combined with great distress in seeing applications of quantum mechanics excessively beyond the conditions of original conception and verification, such as its widespread abuse for energy releasing process that are notoriously irreversible, thus not exactly treatment with a structurally reversible mechanics, such as quantum mechanics, or the application of the theory to biological structures despite their known complexity beyond our imagination at this time.
Similarly, I had great intellectual excitement in studying the Riemannian representation of gravity due to its beauty that has attracted so many colleagues, with great distress due to the absence in the technical literature of any serious study on a number of insufficiencies, such as: the clear insufficiencies for interior gravitational problems compatible with other physical laws (e.g., thermodynamical laws); the impossibility to represent the free fall or our weight with curvature; not to mention structural problems in the time evolution due to curvature. In the final analysis, the sole known impossibility for curvature to allow any consistent grand unification and quantization of gravity constitutes pressing arguments to seek alternative theories of gravitation.
Yet, the most distressing studies have been for me those in 20th century cosmology. To begin, the Greek meaning of the word "cosmos" requires the inclusion of all creation. Therefore, I have difficulties in accepting the very name "cosmology" without at least a primitive treatment of biological structures and antimatter. As it is well known, both these fields were generally ignored in virtually all "cosmological" models of the 20th century, due to their primary intent to adapt the entire universe to Einstein special and general relativities.
My distress grew with the study of models that, even when restricted to matter, lacked any representation of the very important part of cosmology, the irreversible character of all interior gravitational problems for stars, quasars ands black holes. More recently, my distress reached its climax when I realized that, rather than at least considering well known limitations of 20th century theories, true hyperbolas were voiced for the intent of adapting the universe to preferred theories.
The above series of distressing aspects forced me to conduct independent studies. The admission of interior non-Hamiltonian effects forced me to construct isomathematics, and then formate isomechanics and isochemistry reviewed earlier in this work. The inclusion of antimatter via their isodual images allowed the formulation of the isoselfdual isocosmology (ISIC) that, at the limit case of equal amount of matter and antimatter in the universe, is based on the following main axioms:
Isocosmological Axiom I: All events in the universe verify the direct product of the Lorentz-Poincare'-Santilli isosymmetry and for matter and its isodual for antimatter
Isocosmological Axiom II: All events in the universe verify isorelativity for matter and its isodual for antimatter, thus including isogravitation.
Main advances over conventional cosmological models are: the inclusion of antimatter; a more realistic treatment of interior problems; and the elimination of curvature in favor of the isoflatness of the Minkowski-Santilli isogeometry permitting a consistent grand unification as well as operator formulation of gravity; and the resolution of the inconsistencies inherent in the expansion of the universe, "dark matter" and "dark energy.".
Despite these advances, the insufficiencies of the isoselfdual isocosmology were for me as distressing as conventional models, evidently because of the lack of an axiomatically rigorous representation of irreversibility, as well as insufficiencies for the inclusion of biological structures.
In the hope of at least initiating the resolution of these limitations, I was forced to study the isoselfdual genocosmology (ISGC) based in the covering genomathematics with an ordering forward or backward in all operations, resulting in Lie-admissible/Jordan-admissible genomathematics, genomechanics and genochemistry for matter and their isoduals for antimatter.
A main advantage in passing from the isoselfdual isocosmology to the genotopic covering is the first known compatibility of interior gravitational problems with thermodynamic. in fact, being structurally irreversible, genomechanics is the first known mechanics directly compatible with all known thermodynamical laws.
Despite the advance, I remained distressed by the use of the word "cosmology" because of the inability to include biological structures due to insufficiencies of genomethods. An additional reason for distress was the absence of multivaluedness of the universe. In fact,as stressed in the technical literature of the field, any consistent classical representation of antimatter requires its formulation in a space coexistent with, but different than our spacetime. Consequently, the inclusion of antimatter in cosmological studies requires the use of multivalued hyperstructures in their simplest possible form, that characterized by the two valued hyperunit If = (If, Ifd). The transition from such a simple structure to a general multi-valued hyperstructure yields the isoselfdual multivalued hypercosmology (ISMVHC).
It is important to recall here the inevitability of the ether as a universal substratum, and the characterization of matter as vibrations of the same in order to avoid the "ethereal wind" of the 19th century. The existence of different but coexisting multi-valued universes is then a question of admitting incoherent basic frequencies for matter belonging to one universe passing though matter belonging to another universe without interaction or mutual visibility. Note the insistence in the "multi-valued," rather than "multi-dimensional" character, according to which in the former case we have different universes all coexisting with our (3 + 1)-dimensional spacetime, while in the latter case we have universes with dimensions of the generic type (n + 1).
The advances permitted by ISMVHC are rather significant, because of the inclusion of biological structures treated in the most general known way, as well as matter and antimatter in their most general possible irreversible and multi-valued formulation admitting as a particular case special relativity and its isodual for massive points propagating in vacuum.
To the best of my knowledge, the ISMVHC is the most general possible formulation of cosmology permitted by current mathematical, physical and chemical knowledge under the conditions of admitting a universal invariance (to prevent the Theorems of Catastrophic Inconsistencies of Noncanonical and Nonunitary Theories), and the formulation on a hyperfield, (to admit numerical predictions verifiable with experiments).
There is do doubt that, in view of such a vast structure, it may well take some time to surpass the ISMVHC via a broader formulation still admitting a universal invariance as well as applicability to experimental measurements. Yet, I believe that the complexities of the "cosmos" intended as encompassing all creation, are simply beyond our imagination at this writing. Consequently, short of the ascientific adaptation of new, hitherto unknown conditions to a preferred theory, I have no doubt that the ISMVHC will indeed require structural broadening at some future time.
In the final analysis, only artists such as Michelangelo, have produced eternal art. By comparison, we physicists can at best hope to have discovered one mere link in an open ended chain of links that will be continued until the end of mankind.
Appendix 5.7A: Newton-Santilli universal gravitation
Santilli has repeated indicated in his writings that the bending of light by a matter star is entirely due to Newton's gravitation, and not to curvature of space. Alternatively, the representation of the bending via curvature in a Riemannian space leads to inconsistencies, e.g., inability to reproduce in first approximation Newton's attraction of light.
The above statement is generally obscure to physicists because Newton's attraction has been written since its inception in the 1687 Principia in the familiar form
where g is the familiar gravitational constant, which formulation has been applied over four centuries solely to masses, thus excluding light due to its massless character.
In his 2007 paper
Absence of universe expansion, dark matter and dark energy in the new isocosmology with a universal isosymmetry
R. M. Santilli, in the Proceedings of the 2007 ICDS, C. Ozel and V. Cay, Editors, International Academic Press (2007).
Santilli has shown that Newton gravitation is indeed "universal," thus including light. This historically and scientifically important clarification has been reached via the following re-formulation of Newton's law, today called Newton-Santilli universal gravitation
where
is the new gravitational constant.
In essence, Santilli has shown that the gravitational field is not originated by mass m, but by its energy E = mc2. As a an illustration, Santilli points out that the source in the Einstein-Hilbert gravitational field equations is given by the "energy-momentum" tensor, and not by the "mass-momentum" tensor, and that the insistence in the use of the mass as origin of the field leads to various inconsistencies.
Once the origin of the gravitational field is identified with the energy, rather the mass, it is evident that gravitation is indeed universal, thus attracting matter as well as light. In fact, a given light with photon energy E1 = hf is attracted by a matter star with energy E = E2 = mc2 according to the Newton-Santilli law
The proof that the bending of light is entirely of Newton-Santilli character is then elementary. Despite its simplicity, the implications of Santilli's universal re-formulation of Newton's gravitation are indeed momentous, such as:
1) The Newton-Santilli gravitation removes the historical motivation for the assumption that space is actually curved as assumed by Einstein himself. It is hoped interested historians may study the case and clarify whether Einstein did actually believe that Newton's gravitation excluded light, thus not being universal, or Einstein was motivated by other reasons.
2) Newton-Santilli gravitation predicts that the isodual light emitted by an antimatter star is repelled by a matter star and vice-versa. in fact, under isoduality, the energy of a photon becomes negative although referred to a negative unit of energy, according to the law
thus allowing the initiation of antimatter astrophysics that was absent in the 20th century.
3) The Newton-Santilli law of universal gravitation requires a structural revision of a number of additional beliefs in the 20th century astrophysics and cosmology. As shown in Section 5.5, Einstein energy equivalence has been solely established for massive points moving in vacuum under the maximal causal speed c. For extended astrophysical bodies, we expect maximal causal speed (3.95), i.e.,
Santilli's energy equivalence is then given by
where n3 can be assumed to have the value 1 in first approximation. The important point is that in the interior of astrophysical bodies, the value C is, in general, much bigger than c, and the space characteristic functions are bigger than one. Consequently, the gravitational field predicted by the Newton-Santilli law for a given mass is much bigger than that predicted by Newton's or Einstein's gravitation.
To illustrate the far reaching implications, it is sufficient to indicate that the Newton-Santilli law requires a revision of the numerical values of the masses of the constituents of the Solar system. As pointed out by Santilli in the above quoted paper, this is due to the fact that the trajectories of planets in the Solar system have been computed with Newton's law. Since these trajectories cannot be altered, the reinterpretation of Solar data via the Newton-Santilli law requires a revision of the masses, generally expected to be lower than their currently assumed value.
It is hoped this appendix provides additional illustrations of the momentous implications of Santilli studies.