MATHEMATICAL, PHYSICAL AND CHEMICAL SCIENCES
UNDERLYING SANTILLI'S INTERMEDIATE NUCLEAR
SYNTHESES, WITHOUT RADIATIONS
Full scientific presentation available in the monograph
I. Gandzha and J Kadeisvili,
New Sciences for a New Era:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli, Sankata Printing Press, Nepal (2011),
http://www.santilli-foundation.org/docs/RMS.pdf
CHAPTER 1:
INSUFFICIENCIES OF THE 20-TH CENTURY THEORIES
1.1. THE LEGACY OF LAGRANGE AND HAMILTON.
1.2. INSUFFICIENCIES OF SPECIAL RELATIVITY
1.3. INSUFFICIENCIES OF GENERAL RELATIVITY
1.4. INSUFFICIENCIES OF EINSTEIN'S THEORIES FOR ANTIMATTER
1.5. INSUFFICIENCIES OF QUANTUM MECHANICS
1.6. INSUFFICIENCIES OF NUCLEAR PHYSICS
1.7. INSUFFICIENCIES OF PARTICLE PHYSICS
1.8. INSUFFICIENCIES OF QUARKS AND NEUTRINOS CONJECTURES
1.9. INSUFFICIENCIES OF QUANTUM CHEMISTRY
1.10. INSUFFICIENCIES OF BIOLOGY
1.11. INSUFFICIENCIES OF ASTROPHYSICS AND COSMOLOGY
1.12. INTRODUCTORY READINGS
CHAPTER 1:
INSUFFICIENCIES OF THE 20-TH CENTURY THEORIES
1.1. THE LEGACY OF LAGRANGE AND HAMILTON.
Santilli conducted his graduate studies in theoretical physics in the late 1960s at the University of Torino, Italy, where J. L. Lagrange lived and did some of his research. In this way, Santilli had the opportunity of studying the original papers by Lagrange (some of which had been written in Italian), thus learning Lagrange's original conception of his celebrated analytic representation of nature (dating to 1788) as requiring two quantities:
1) A function L(r, v) = K(v) - V(r), today known as the Lagrangian, where r = (rk), k = 1, 2, 3, are the coordinates, v = dr/dt represents the velocity, K(v) = mv2/2 is the kinetic energy, and V(r) represents all action-at-a-distance forces derivable from a potential, plus
2) The external terms, F(t, r, v), that is, terms external to his analytic equations representing all forces not derivable from a potential or a Lagrangian.
Santilli then studied in British libraries the original works by W. R. Hamilton and discovered that in 1834 he had essentially the same conception as that by Lagrange for the analytic representation of nature as characterized by a function, today known as the hamiltonian representing the total energy in a space (today called cotangent bundle) with local coordinates r and p = m v,
plus his celebrated analytic equations, those with external terms representing forces non-derivable from a potential (hereon called "non-Hamiltonian forces"),
The above analytic representation of nature remained in full force and effect until the early 1900. As an example, C. G. Jacobi formulated his celebrated theorem in 1837, not in the form presented in mechanics books of the 20th century where the external terms are generally removed, but for the true Lagrange and Hamilton equations, those with external terms.
The advent in the early 1900 of special relativity and quantum mechanics caused a major alteration of the original analytic conception of nature by Lagrange and Hamilton. In essence, both special relativity and quantum mechanics are strictly Hamiltonian theories, that is, they only admit one quantity, a Lagrangian or, equivalently, a Hamiltonian for the entire representation of a system, and show no possibility of accommodating the external terms short of a major structural revision.
Consequently, the widespread posture of the 20th century physics was to eliminate Lagrange and Hamilton external terms and solely work with equations today called the truncated Lagrange and Hamilton equations. A general argument was that the forces represented by the external terms are "fictitious" (sic) because, the argument says, when a system in our environment is reduced to its elementary constituents, all non-Lagrangian or non-Hamiltonian forces "disappear" (sic) and nature assumes the analytic structure of the truncated equations.
The first historical scientific contribution by Santilli was to formulate and prove the following theorem showing that the above posture is a mere manifestation of academic politics without scientific credibility. Santilli initiated his research on the following theorem in the late 1960s (see Refs. [30,31,32]); he continued them in 1978 in memoirs [41,42] at the foundations of hadronic mechanics; and he finalized them in various papers (see, e.g., memoir [92] published by the {\it Italian Physical Society} herein adopted) and in various books (see Refs. [11,12,13]).
THEOREM 1.1: A macroscopic system with forces that are nonconservative and/or irreversible over time cannot be consistently decomposed into a finite number of elementary particles all with solely conservative forces derivable from a potential and, vice versa, a finite number of elementary particles all in conservative conditions cannot consistently yield, under the correspondence principle or other means, a macroscopic system with nonconservative and/or irreversible forces.
The importance of this theorem is set by the fact that the non-Lagrangian or non-Hamiltonian forces of our macroscopic environment, rather than "disappearing" at the particle level to please academia, originate at the most elementary level of nature, thus confirming the depth of the analytic conception of nature by Lagrange and Hamilton.
As an illustration, Santilli's Theorem 1.1 establishes that the resistance experienced by a spaceship during re-entry in our atmosphere is due to the superposition of a large number of contact, nonlinear, nonlocal and nonpotential interactions between the peripheral atomic electrons of the spaceship and corresponding atomic electrons in the atmosphere.
Another significance of Santilli's Theorem 1.1 is to establish ab initio that special relativity and quantum mechanics are not universal theories valid for all possible conditions in nature until the rest of time, as essentially implied by a widespread posture of the 20th century science, but have instead clear limitations.
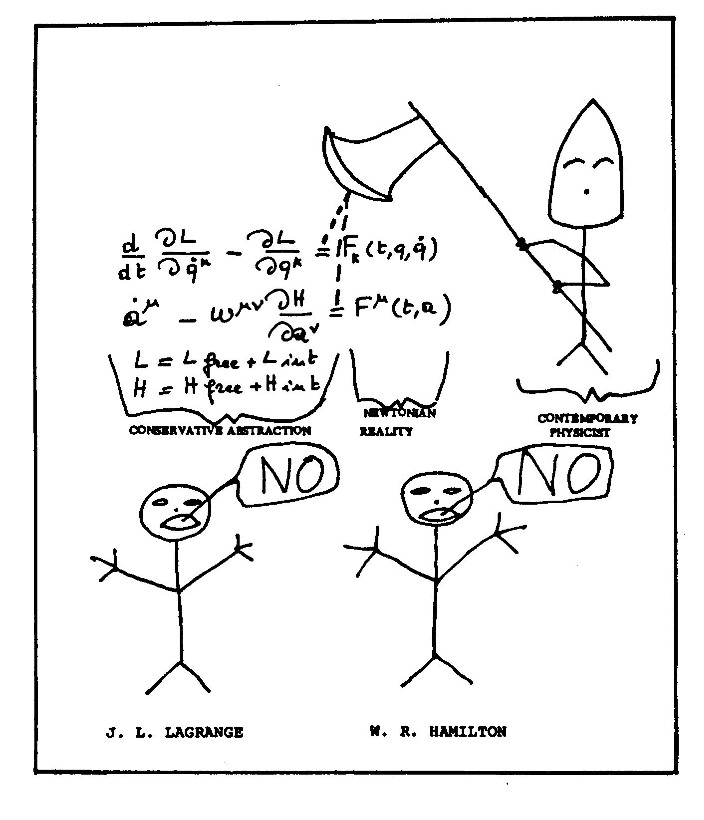
Figure 1.1. The "vignette" presented by Santilli to his colleagues at the Lyman Laboratory of Physics of Harvard University at the initiation of his stay there in September 1977, as part of his research program under DOE support, illustrating the need to study Lagrange's and Hamilton's legacy. This study encountered extreme oppositions at Harvard University due to known irreconcilable incompatibilities of Lagrange's and Hamilton's external terms with Einsteinian doctrines. quantum mechanics, quantum chromodynamics and all that (for details, see the Ethical Notes of Sections 3.10, 3.11 and 3.12).
Numerous additional historical implications of Theorem 1.1 will be indicated throughout this presentation. At this moment, we merely mention the huge technical difficulties caused by the inclusion of external terms in the analytic equations. In essence, the physics of the 20th century was based on Lie algebras with antisymmetric brackets [A, B] = - [B, A] that appear in the time evolution of a physical quantity Q(r, p) of the truncated Hamilton's equations, dQ/dt = [Q, H], where the brackets are the celebrated Poisson brackets. The appearance of Lie algebras at the foundation of dynamics, the time evolution, then allowed a rigorous construction of the various aspects of special relativity and quantum mechanics.
Santilli identified since his graduate studies (see the above quoted references) that, when the external terms are added to the analytic equations, the time evolution of a quantity Q(r, p) is given by
where [Q, H] are the Poisson-Lie brackets. The huge technical difficulties are then set by the fact that, when the brackets [Q, H] of the truncated equations are extended to the brackets (Q, H) of the true analytic equations, there is the loss of all possible algebras, let alone all Lie algebras, in the brackets of the time evolution because the new brackets (Q, H) violate the conditions for the characterization of an algebra (the distributive and scalar laws).
The loss of all algebras in the time evolution then causes the irreconcilable inapplicability of all Hamiltonian methods and theories developed in the 20th century, including special relativity and quantum mechanics.
Rather than being discouraged by this occurrence, in the 1960s Santilli set as his main research goal the development of covering mathematical and physical theories suitable for the implementation of Lagrange and Hamilton analytic conception of nature while restoring an algebra in the brackets of the time evolution.
This presentation is essentially a review of Santilli's studies conducted since that time to achieve the above goal and identify its main implications in various quantitative sciences, as well as its industrial applications for much needed new clean energies and fuels that motivated Santilli's entire body of research. As he puts it in his works: Quantitative sciences will never admit final theories. No matter how beautiful any given theory may appear, its structural generalization is only a question of time.
In the rest of this chapter we review essentially ad litteram the insufficiencies of all quantitative sciences of the 20th century identified by Santilli as the necessary pre-requisite for their resolution via his covering theories, as presented, for instance, in monograph [19].
1.2. INSUFFICIENCIES OF SPECIAL RELATIVITY
Santilli has repeatedly stated in his writings that special relativity has a majestic axiomatic structure, for which reason he assumed said axioms for his covering relativities.
However, a widespread belief in the physics of the 20th century has been that special relativity is valid under whatever conditions exist in the universe, to such an extent that the universe has been often adapted to verify special relativity, rather than adapting the theory to physical reality, with consequences that can only be qualified as characterizing a serious scientific obscurantism.
An important contribution made by Santilli in physics has been the identification of:
1) The conditions of clear validity of special relativity, given by the conditions originally conceived by the founding fathers, namely, for point-particles and electromagnetic waves propagating in vacuum (empty space) or, equivalently, by all conditions in which particles can be well abstracted as being point-like, such as the electron in the hydrogen structure, particles in accelerators, and many other systems;
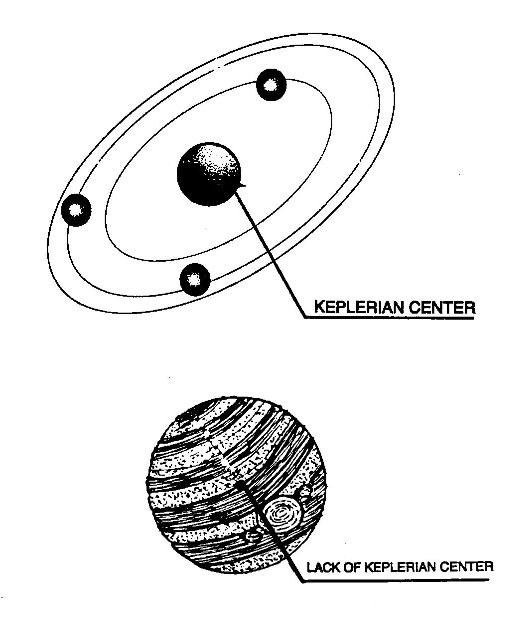
Figure 1.2. A schematic illustration presented by Santilli various times on: the distinction between exterior and interior dynamical problems (see Section 3.12 for definitions); Santilli's s acceptance of special relativity for the characterization of Keplerian systems, such as atomic or planetary structures; and Santilli's impossibility to accept special relativity for interior problems, such as those for hadrons, nuclei and stars, due to lack of a Keplerian nucleus with consequential necessary loss of the Lorentz-Poincare' symmetry.
2) The condition of mere approximate character of special relativity, given by all conditions of particles at mutual distances equal or smaller than their wavepacket or charge distributions or, equivalently, for the motion of particles and electromagnetic waves within physical media, such as liquids, atmospheres, chromospheres, or the hyperdense media inside hadrons, nuclei and stars. These conditions cause mutual penetrations of wavepackets and charge distributions under which particles cannot be effectively approximated as being dimensionless points due to contact, nonlinear, nonlocal and non-Hamiltonian effects expected from Theorem 1.1 and other reasons reviewed in Chapters 3-9. In particular, special relativity can only be approximately valid for the structure of hadrons, nuclei and stars (see Figure 1.2);
3) The conditions of inapplicability of special relativity (and not violation because the theory was not conceived for that), such as the classical representation of antimatter (see Section 1.4), irreversible systems such as energy releasing processes, (due to the strictly reversible character of special relativity compared to the strict irreversibility over time of the processes considered), and other conditions presented in Chapter 3.
It should be indicated that Albert Einstein identified quite clearly in his writings the above indicated Conditions 1 for the applicability of his studies. The extension of special relativity to conditions dramatically beyond those identified by Einstein without a serious scrutiny has been perpetrated by Einstein's followers, who are indeed responsible for the scientific obscurantism indicated earlier and documented in more details in the rest of this presentation.
1.3. INSUFFICIENCIES OF GENERAL RELATIVITY
Unlike his view on special relativity, Santilli believes that Einstein's conception of gravitation via a curved space, despite its unquestionable mathematical beauty, is one of the most controversial theories in history, with fundamental, yet unresolved physical inconsistencies.
This severe view is motivated by various quantitative studies indicated in more details in Chapter 3. At this introductory stage, we recall Santilli's confirmation that the Riemannian geometry provides a good mathematical description of gravity, but Santilli is unable to accept space as being truly curved by gravitation in the actual physical sense because of:
1) The impossibility of representing with curvature the weight of bodies when in stationary conditions;
2) The impossibility of representing with curvature the free fall of bodies along a straight radial line;
3) The absence of curvature in the bending of light when passing near a celestial body, since that curvature is due to Newtonian attraction, rather than curvature of space as we shall see in Chapter 5, and other reasons.
At a deeper level, it should be recalled that special relativity is physically consistent because it verifies the crucial condition of invariance over time, namely, the prediction of the same numerical values under the same conditions but at different times, which invariance is ultimately due to the canonical-Hamiltonian structure of the theory and to its invariance under the Poincare' symmetry.
By contrast, Santilli has proved that the Riemannian geometry does not yield numerical values invariant over time because of the well known fact that the conception of gravitation on a curved space requires a "covariance," rather than a strict invariance, with consequential alteration of numerical values under the same conditions at different times (Section 3.9).
Additionally, the predictions of special relativity under given conditions are unique. By contrast, Santilli has shown that the numerical predictions of general relativity for given conditions are not unique in view of the well known fact that general relativity is a nonlinear theory whose solution requires one or another approximation. It then follows that the numerical predictions depend on the selected expansion as well as the selected parameter for a given expansion.
Santilli has also shown that: general relativity violates the fifth identity of the Riemannian geometry, the Freud identity, for the case of neutral bodies (due to the lack of a source tensor in the exterior problem in vacuum); general relativity is incompatible with quantum electrodynamics (also because of the lack of a source tensor in vacuum for neutral bodies); general relativity verifies the Theorems of Catastrophic Mathematical and Physical Inconsistencies for Noncanonical or Nonunitary Theories (Section 3.9); and the theory has other basic unresolved problems generally ignored by researchers in the field, thus fueling the indicated scientific obscurantism.
1.4. INSUFFICIENCIES OF EINSTEIN'S THEORIES FOR ANTIMATTER
Another reason for the scientific obscurantism of the 20th century is that special and general relativities were widely believed to apply for all possible conditions existing in the universe, while in reality they are unable to provide a valid classical representation of antimatter,
In fact, said theories can solely represent antimatter via the change of the sign of the charge. Consequently, said theories provide no distinction whatsoever between neutral bodies made up of matter and antimatter. Even when considering charged particles, quantization leads to inconsistencies, due to a resulting "particle" with the wrong sign of the charge, rather than the charge conjugated antiparticle.
In Santilli's words: One of the biggest scientific imbalances of the 20th century has been the treatment of matter at all possible levels of study, from Newton to second quantization, while antimatter was solely treated at the level of second quantization. Hence, he decided to resolve this historical imbalance by discovering a new theory of antimatter that, as it is the case for matter, is applicable at all levels of study from Newtonian mechanics to second quantization, and he did indeed achieve such a goal, as we shall see in Section 3.7.
1.5. INSUFFICIENCIES OF QUANTUM MECHANICS
Santilli has repeatedly stated that quantum mechanics has made historical contributions to mankind, by possessing a majestic axiomatic structure he assumed for the construction of hadronic mechanics, besides having an impressive body of experimental verifications under the conditions of its original conception and construction.
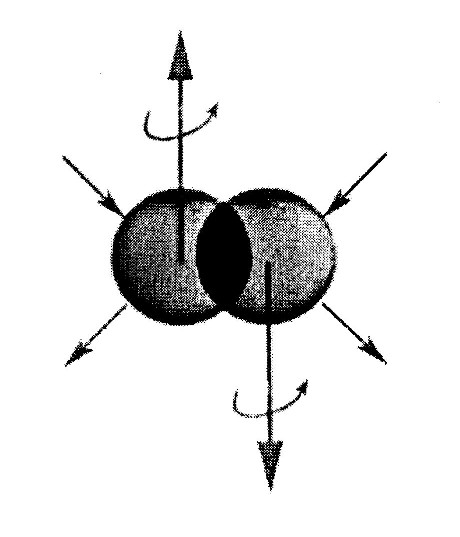
Figure 1.3. The new interactions at the foundations of hadronic mechanics originating from mutual contact and penetration of the wavepackets of particles at short distances that are non-Hamiltonian because nonlinear, nonlocal and nonpotential, thus requiring a nonunitary lifting of quantum mechanics, including its mathematics, physical laws and experimental verifications.
Despite these achievements, physics is a discipline that will never admit final theories valid to the end of time. In fact, Santilli became a physicist because of authoritative doubts on the final character of quantum mechanics expressed during his high school years even in the Italian press for the general public, such as:
A) The view by Albert Einstein on the "lack of completion" of quantum mechanics (in fact, Santilli constructed hadronic mechanics precisely as a "completion" of quantum mechanics in honor of Albert Einstein);
B) The doubts expressed by Enrico Fermi as to whether quantum mechanics holds in the interior of mesons (Santilli quoted repeatedly Fermi's doubt as being at the foundation for his studies on the structure of hadrons);
C) The limitations of quantum mechanics voiced by Werner Heisenberg, one of the very founders of the mechanics, from the linear character of the theory compared to the evident nonlinearity of the physical world (Santilli corresponded with Heisenberg on this topic prior to Heisenberg's death in 1976);
D) The authoritative doubt voiced by Paul M. Dirac, another major founder of quantum mechanics, on the need for a revision of the theory permitting convergent perturbative expansions (Santilli met Dirac in Florida in 1982 to discuss the capability of hadronic mechanics to turn divergent quantum series into convergent forms, as reported by Santilli in his books);
E) The arguments by various philosophers of science on the need to surpass quantum mechanics with broader theories, such as Karl Popper, who was a strong supporter of Santilli's proposal to build the hadronic covering of quantum mechanics, as stated in the Preface of his last book of 1978; and other doubts.
With the passing of time, these authoritative doubts were first ignored; then the authors were discredited via the abuse of academic authority, including the discreditation of Heisenberg, Dirac, Popper and other famous scientists for the lack of alignment of their views with the predominant political lines of the academic time; and any additional qualified doubt was prohibited to appear in print in the journals of leading physical societies, while its appearance in the press was opposed or discredited.
This evident organized manipulation of scientific knowledge and suppression of scientific democracy of qualified inquiries for personal interests led to the widespread assumption in the last part of the 20-th century that quantum mechanics (and its Galilean and special relativity backgrounds) are the final theories for all possible conditions existing in the universe to the end of time, resulting in a manifest scientific obscurantism of historical proportions.
It is a duty of future historians to identify the reasons for the suppression of these authoritative doubts, as well as the responsibilities by leading academic institutions and governmental agencies funding the research, by identifying the origination of the rather universal trend of adapting all possible conditions in the universe to verify quantum mechanics and its underlying relativities.
A notorious exception is that by Santilli who honored the indicated authoritative doubts, conducted comprehensive mathematical, theoretical and experimental research on the limitations as well as the surpassing of quantum mechanics in a way completely oblivious to organized ascientific interests, and did indeed change the history of physics, as we shall see.
To begin our review in the field, another major scientific contribution by Santilli has been the restoration of a serious scientific process on quantum mechanics and its underlying relativities as follows:
1) A theory is said to be exactly valid for given conditions when it represents the totality of the physical data from primitive axioms without adulterations (such as throwing into the equations unknown parameters, arbitrary functions, and the like). This is the case for the structure of the hydrogen atoms, particles in accelerators, crystals, and numerous other systems. By analyzing the local-differential topology and mathematics underlying the theory, Santilli has confirmed that the conditions for the exact validity of quantum mechanics are the same as those for special relativity (as expected from the deep synergy of these theories), namely, quantum mechanics can be safely assumed to be exactly valid for particles and electromagnetic waves propagating in empty space or, more generally, for particles at mutual distances sufficiently bigger than their size and/or charge distribution to allow their effective point-like abstraction.
2) A theory is said to be approximately valid when the representation of experimental data requires ad hoc parameters and/or arbitrary functions that are then fitted from the data themselves (this is the case for numerous events in particle physics, nuclear physics, astrophysics and other disciplines). In particular, Santilli has proved that said arbitrary parameters and/or functions are, in reality, a direct measure of the deviations of the basic axioms of the theory from the system at hand. Numerous illustrative examples in both quantum mechanics and quantum chemistry were then worked out (see the Chapters 3, 4, 5).
3) A theory is said to be inapplicable (rather than "violated") when the parameters thrown into the equations are incompatible with the basic axioms, or the theory does not admit any quantitative representation at all of experimental data. Illustration cases of inapplicability of quantum mechanics are the following:
3A) The use of the four parameters (called "chaoticity parameters") necessary for the quantum mechanical representation of the experimental data via the Bose-Einstein correlation is prohibited by quantum axioms, because the two point correlation function for a two-dimensional Hermitean (thus diagonal) operator could at best admit two parameters. Hence, the additional two parameters needed for the representation must be off-diagonal, thus being in direct violation of the axiom of vacuum expectation values for a Hermitean operator;
3B) Quantum mechanics is inapplicable for the synthesis of the neutron from a proton and an electron as occurring in stars because, in this case (kept quite secret by academia, the Schroedinger equation becomes inconsistent, an occurrence that is the historical motivation for the very birth of the covering hadronic mechanics, as we shall see;
3C) Quantum mechanics is inapplicable for all processes that are irreversible over time, such as nuclear fusions, because quantum mechanics is reversible over time, thus admitting the time reversal event (such as the synthesized nucleus spontaneously decomposing itself into the original two nuclei) with embarrassing violations of energy conservation, causality and other basic laws.
By looking in retrospect at a lifetime of research, we can quote Santilli's statement that: The selection of the appropriate generalization of quantum mechanics for physical conditions more complex than those of its conception and experimental verification, should indeed be the subject of scientific debates, but the aprioristic assumption of quantum mechanics as being exact for all conditions existing in the universe is ascientific, amoral and asocial, particularly when ventured by physicists at leading academic institutions.
1.6. INSUFFICIENCIES OF NUCLEAR PHYSICS
The contributions of quantum mechanics to nuclear physics are well known, the most notorious being the atomic bomb and nuclear power plants. Santilli points out that these events deal with fission processes whose debris admit a good approximation as being point-like, thus allowing quantum mechanics to be effective.
As a result of said historical achievements, quantum mechanics was assumed throughout the 20-th century as being exactly valid for all possible nuclear structures and processes. Yet, Santilli pointed out that quantum mechanics cannot possibly be exactly valid for fusion processes, since the theory is reversible over time. Thus, jointly with the probability of nuclear syntheses of two nuclei into a third, N1 + N2 → N3 plus energy, quantum mechanics admits a finite probability for the spontaneous time reversal reaction
in fragrant disagreement with the conservation of energy and other laws, trivially, because the probability amplitude does not depend explicitly on time.
With the understanding that the approximate validity of quantum mechanics in nuclear physics is out of question, Santilli believes that one of the most pernicious manifestations of the scientific obscurantism of the 20th century existed in nuclear physics, due to the religious assumption of the exact validity of quantum mechanics in the field when quantum mechanics has failed to achieve an exact representation of all experimental data of the simplest possible nucleus, the deuterium, because:
1) Quantum mechanics has been unable to represent the spin 1 of the deuterium since quantum axioms require that the sole stable bound state of two particles with spin 1/2, the proton and the neutron, must be the singlet state with spin zero;
2) Quantum mechanics has been unable to represent the magnetic moment of the deuterium despite 100 years of research and the use of all possible relativistic corrections;
3) Quantum mechanics has been unable to explain the stability of the neutron when coupled to the proton in the deuterium, since the neutron is a naturally unstable particle (when isolated) with about 14 minutes lifetime; and other insufficiencies.
The assumption of quantum mechanics as being exactly valid in nuclear physics reaches historical proportions when proffered by experts in the field from authoritative academic institutions, or by editors of leading physics societies, when one considers that the huge deviations of quantum mechanics from the experimental data of large nuclei, such as the zirconium.
Santilli qualifies as distressing the inability by quantum mechanics to reach a serious understanding of the nuclear force, because quantum mechanics is strictly Hamiltonian, as indicated above. Hence, all research over the past century has been studiously restricted to represent the nuclear force with a potential. The impossibility of representing experimental data then forced the addition of more and more potentials, to the extreme that nuclear forces have recently reached up to 35 different potentials without achieving the needed exact representation,
+ V11 + V12 + V13 + V14 + V15 + V16 + V17 + V18 +
+ V19 + V20 + V21 + V22 + V23 + V24 + V25 +
+ V26 + V27 + V28 + V29 + V30 + V31 + V32 +
+ V33 + V134 + V35 + ...
To express his distress, Santilli states: There is a limit in the political manipulation of scientific knowledge and its adaptation to preferred theories, rather than adapting the theories to physical reality no matter how beloved the theories are, beyond which limit all credibility is lost to such an extent of raising issues of scientific ethics and accountability, particularly when the manipulation is perpetrated under public financial support. In fact, the insufficiency of potentials to represent nuclear forces squarely brings into focus Santilli's Theorem 1.1. on the origin of nonconservative / nonpotential forces at the very structure of matter, thus including nuclear structures.
Above all, Santilli has never accepted quantum mechanics to be exactly valid for nuclear physics because its basic symmetries, the Galilei and the Poincare' symmetries, solely apply for Keplerian systems, thus requiring a nucleus, and states: Quantum mechanics cannot possibly be exactly valid for nuclear structures because nuclei do not have nuclei, as a consequence of which the basic Galilean and Poincare' symmetries must be broken, thus causing incontrovertible deviations from quantum axioms.
As we shall see in Chapter 3, the "completion" of quantum mechanics into a covering mechanics achieving an exact representation of nuclear data permits the prediction and quantitative treatment of new clean energies so much needed by our society. Hence, the resolution of the approximate character of quantum mechanics in nuclear physics has major societal, let alone physical relevance.
By following Santilli, we can again state that the selection of a mechanics more adequate than quantum mechanics for nuclear structures should indeed be the subject of scientific debates, but the aprioristic assumption of quantum mechanics as being exactly valid in nuclear physics creates serious problems of scientific ethics and accountability (with inevitable legal overtones).
1.7. INSUFFICIENCIES OF PARTICLE PHYSICS
In Santilli's view, the biggest scientific obscurantism exists in particle physics with particular reference to claimed "experimental results" for high and very high energy particle collisions, and/or deep inelastic scattering, that he calls "experimental beliefs."
The argument is that all these data are based on the use of the conventional potential scattering theory, namely, a theory based on the religious assumption that particles remain point-like also under very high energy collisions (a condition necessary to apply quantum mechanics) and, as such, the particles solely experience action-at-a-distance interactions derivable from a potential.
In his own words, Santilli states: According to the axioms of quantum mechanics and their consequential point-like abstraction of particles, neutral particles can have no scattering at all since dimensionless points cannot affect the trajectory of other dimensionless points, while charged particles can only have Coulomb scattering at all energies. Therefore, the very existence of deviation from these basic lines in scattering experiments establishes beyond credible doubt the presence of non-Hamiltonian effects in deep mutual penetrations of the wavepackets and/or charge distributions of particles.
The electron has an extended wavepacket irrespective of its point-like charge. But at sufficiently low mutual distances, electrons have scattering trajectories departing from the Coulomb behavior, thus establishing on serious scientific grounds beyond academic politics that the conventional, potential scattering theory can only be approximately valid for high energy scattering experiments, since it is notoriously unable to incorporate nonpotential / non-Hamiltonian effects due to mutual wave overlappings.
When passing from the electron point-like charge to scattering experiments of particles with extended charge distributions such as hadrons, the insufficiencies of the conventional potential scattering theory raise clearly historical problems of scientific ethics and accountability due to very large public sums current spent by high energy physics laboratories around the world that release "experimental beliefs" without any serious appraisal of the theoretical theologies used for the claimed results.
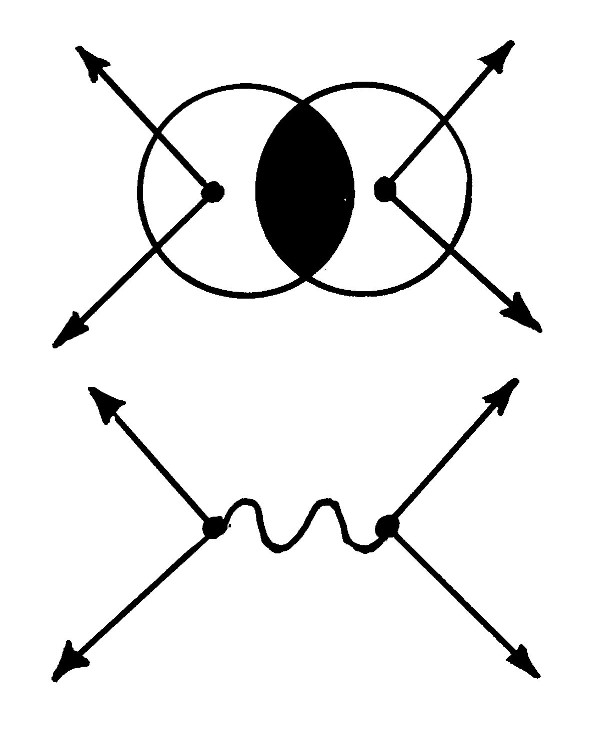
Figure 1.4. An illustration of the reason Santilli cannot accept the experimental data, let alone the basic theories, of the 20th century particle physics, illustrating the point-like abstraction of particles and their wavepackets (below), compared to the necessary deep overlapping of said wave-packets and/or charge distributions in high energy scattering experiments (above). Incontrovertible experimental evidence for deviations in scattering experiments from a point-like behavior establish the merely approximate character of the potential scattering theory and related lack of final character of the claimed "experimental results." Additionally, Santilli cannot accept 20th century particle physics due to its irreconcilable incompatibility with other branches of physics, such as: incompatibility with Newtonian mechanics due to Theorem 1.1; incompatibility with thermodynamics due to the strict reversibility over time of particle physics compared with the irreversibility of thermodynamics; etc,
We hope the reader begins to see in this way additional historical implications of Santilli's Theorem 1.1, since it requires the emergence of nonpotential forces precisely at the level of deep inelastic scattering or collisions, as it is the case of the spaceship during re-entry in our atmosphere. But these forces are non-Hamiltonian, thus requiring a necessary nonunitary covering of the scattering theory, which is one of the primary objective of hadronic mechanics in view of its nonunitary structure.
Whatever nonunitary scattering theory emerges to be correct for high energy particle scattering experiments, it is clear that it will mandate a re-inspection of all "experimental beliefs" in particle physics to ascertain whether the results claimed under sole potential forces are exact or merely approximate, thus in need of basic revisions of the numerical results.
1.8. INSUFFICIENCIES OF QUARKS AND NEUTRINOS CONJECTURES
Santilli has always accepted SU(3)-color theories as providing the final Mendeleev-type classification of hadrons into families; has accepted quarks as being necessary for the elaboration of said Mendeleev classification; but he has never accepted quarks as being physical particles actually existing in our spacetime for numerous reasons, such as:
a) Quark can only be technically defined as purely mathematical representations of a purely mathematical internal symmetry, defined on a purely mathematical internal, complex-valued unitary space, without any possibility of being consistently definable in our spacetime (because prohibited by the Poincare' symmetry and other reasons);
b) Quarks cannot have any gravity because, as stated by Albert Einstein, gravity can be solely defined for masses in our spacetime, while quarks cannot be seriously defined in our spacetime.
c) Nuclei, atoms and molecules have required one model for their classification into family and a different, yet compatible model for the structure of each individual element of a given family, and the same occurrence is expected for the classification and structure of hadrons.
To illustrate the basic dichotomy classification versus structure, Santilli has stated that: If one of my graduate students would ask me to supervise a thesis whereby the Mendeleev table for atoms is also used for the structure of each individual atoms of a given family, I would immediately request his/her expulsion from the department, because classification and structure are dramatically different problems, requiring dramatically different methods and theories.
In fact, the Mendeleev table was formulated via classical chemical and other methods, while the structure of the atoms required the advent of quantum mechanics. As we shall see, we have a very similar situation for hadrons because the linear, local and Hamiltonian character of quantum mechanics is effective for the classification of hadrons under their point-like approximation, but the same mechanics has been shown to be inadequate for structure problems due to inevitable nonlinear, nonlocal and non-Hamiltonian effects occurring within hyperdense media inside hadrons.
Santilli has additionally stated: According to the standard model, at the time of the neutron synthesis from protons and electrons inside a star, the permanently stable protons and electrons simply "disappear" (sic) from the universe to be replaced by conjectural quarks, and then the proton and the electron simply "reappear" (sic) at the time of the neutron decay. These beliefs are simply repugnant to me because excessively irrational, thus showing the conduction of particle physics via academic authority, rather than scientific veritas.
Similarly, Santilli never believed that the neutrinos are physical particles in our spacetime for numerous reasons, the first being the fact that the neutrino is assumed to be emitted during the synthesis of neutrons from protons and electrons inside stars,
while a more correct assumption should have been its absorption, because the neutron is 0.782 MeV heavier than the sum of the rest energies of the proton and the electron,
As a result, quantum mechanics is basically inapplicable for any quantitative treatment of synthesis (1.6) for various reasons, such as:
A) All bound states characterized by quantum mechanics (such as nuclei, atoms and molecules) must have a "mass defect," namely, the rest energy of the resulting state must be smaller than the sum of the rest energies of the constituents, resulting in the familiar "negative binding energy." By contrast, reaction (1.6) requires a kind of "mass excess," thus requiring a "positive binding energy," under which the Schroedinger and other equations of quantum mechanics become inconsistent.
B) The assumption of the "missing energy" of 0.782 MeV as being provided by the relative kinetic energy of the proton and the electron is inconsistent and untenable, because at that energy the cross section of protons and electrons is virtually null, thus prohibiting any bound state;
C) The belief that the conjugate expression
where ν† denotes antineutrino (due to the absence in html language of ν-bar), is political and equally inconsistent, because the antineutrino has an identically null cross section with the proton and the electron, thus being unable to provide them the missing energy. In any case, recent studies have established that antineutrinos should have a negative mass referred to a negative unit as a necessary condition to achieve a classical theory of antimatter (see Chapters 2, 3), thus requiring, rather than providing energy for the neutron synthesis.
The advent of the standard model has caused additional, rather serious, unresolved problems because Fermi's original conception of one massless and chargeless neutrino and its antiparticle had to be first extended to three different neutrinos and their antiparticles without any serious identification of their differences; then this enlargement had to be further enlarged to admit that neutrinos have masses; then the latter enlargement had to be further broadened with the additional belief that neutrinos have different masses; then the latter assumption had to be further modified with the conjecture that neutrinos "oscillate" (that is, change from one form into the other); with the expectation of additional unverifiable conjectures introduced to bypass the problems unsolved by the preceding conjectures, yet under very large public funds dispersed at major international laboratories on these pure theoretical theologies without any serious scrutiny by society, thus confirming the ongoing scientific obscurantism.
Any denials of the need for a basic re-inspection of physical laws for the most fundamental synthesis in nature, that of the neutron, can only raise serious problems of scientific ethics and accountability (also with inevitable legal overtones).
Santilli states: Until I live, I will refuse to accept that very large fluxes of massive particles, such as neutrinos originating from stars, are believed to traverse entire planets and stars, thus passing through an enormous number of nuclei, without any collision at all. Instead of accepting such a theology, I will look for alternative theories more plausible than that of the neutrinos. So, in fact, he did, by introducing his theory of "longitudinal" impulses propagating through the ether as a universal substratum, thus explaining the lack of collision (see Chapters 3, 5).
Unreassuringly, Santilli has also stated that: Quarks and neutrinos have been claimed to exist as physical particles in our spacetime by organized high ranking academic interests because their assumption is essential to preserve the validity of special relativity and quantum mechanics.
In any case, the various claims of leading particle laboratories to have "discovered" or "detected" this or that quark is extremely anti-scientific for me because the correct scientific statement should have been that of having detected physical particles in our spacetime "predicted" by quark conjectures, with the understanding that the same particles could be predicted by other conjectures.
In the final analysis, the conjecture that quarks are physical particles in our spacetime prohibits the study of possible new clean energies because quarks must be assumed as being permanently confined in the interior of hadrons, while all energies obtained from nuclear, atomic and molecular structures are based on the capability of extracting the constituents free.
1.9. INSUFFICIENCIES OF QUANTUM CHEMISTRY
As it is well known, quantum chemistry has also made historical contributions to society, but this is no reason to expect that quantum chemistry is the final theory for all chemical processes until the end of time. In fact, , beginning with the time of his graduate studies in the 1960s, Santilli never accepted quantum chemistry as a final discipline for numerous reasons he has identified in his works. For instance, he states that:
The fundamental quantum chemical notion of valence bond, as presented in the 20th century literature, is a pure nomenclature without quantitative content because, to be quantitative, the notion should:
1) Identify clearly the force between two identical valence electrons;
2) Prove that such a force is attractive, as an evident necessary pre-requisite to claim the bond needed for a molecule; and
3) Prove that such a clearly identified clearly attractive force verifies indeed experimental data on molecular structures.
These conditions are impossible for quantum chemistry, because two identical electrons must "repel" each other according to quantum mechanics, and they cannot possibly "attract" each other.
Therefore, Santilli set his goal to achieve the missing quantitative notion of valence, and he did achieve it, as we shall see in Chapter 4, giving birth to the new discipline of hadronic chemistry.
Santilli has also identified additional structural problems of quantum chemistry, among which most visible is the prediction (verified by one of his graduate students) that all substances are paramagnetic, in great disagreement with evidence establishing that only certain substances are paramagnetic.
This insufficiency can be verified with the hydrogen molecule that is indeed diamagnetic. The origin of the problem rests in the absence of a clearly identified, sufficiently "strong" valence bond among the pair of valence electrons of the H2 molecule, as a result of which the orbitals of individual hydrogen atoms remain essentially independent, thus available for a joint polarization via an external magnetic field, contrary to evidence.
Figure 1.5. A view used by Santilli to illustrate the prediction by quantum chemistry that all substances, such as water, are paramagnetic, in dramatic disagreement with evidence. The prediction is a consequence of the lack of a "strongly" attractive force between valence electron "pairs," as occurring in nature, in which absence valence electrons remain essentially independent, thus capable of acquiring a magnetic polarization, of course, under a sufficiently strong external magnetic field. .
Santilli had another graduate student prove that, under the current notion of valence, there is no reason to have the sole molecule H2, since it is possible to bond together three, four or more hydrogen atoms, contrary to evidence. The origin of this additional insufficiency is, again, the lack of a "strongly" attractive valence bond restricting the correlation to valence electron "pairs" only, thus allowing the bonding of additional electrons, contrary to evidence (as we shall see in Chapter 4, the species H3, H4 at times detected in gas chromatography have been proved by Santilli to have a bond other than that of valence).
Additionally, Santilli proved that quantum chemistry cannot be exactly valid for the study of chemical reactions, by showing that, jointly with the prediction of the synthesis of the water molecule H2 + O → H2O, quantum chemistry admits a finite probability for the time reversal event, the spontaneous disintegration of the water molecule into its original constituents,
in dramatic violation of the principle of conservation of the energy. The reason is well know, but kept a great secret in advanced chemistry departments and laboratories, namely, the fact that quantum chemistry is a theory reversible over time, while chemical reactions, such as the synthesis of the water molecule, are strictly irreversible processes.
It is then evident to all serious scholars outside academic politics that quantum chemistry cannot possibly be the final theory for chemistry, the most serious limitations occurring for chemical reactions. Of course, the applicable new chemistry is open to scientific debates, but the denial of its need can only raise issues of scientific ethics and accountability (again, with inevitable legal overtones).
1.10. INSUFFICIENCIES OF BIOLOGY
Among all sciences of the 20th century, that considered most distressful by Santilli is biology treated via quantum mechanics. In fact, he writes: Had quantum mechanics been applicable to biological processes, my body should be perfectly rigid and perfectly eternal.
This insufficiency is due to the well known incompatibility of quantum mechanics with the deformation theory (since deformations would cause the breaking of its central pillar, the rotational symmetry), as a result of which quantum mechanics is ideally suited to represent rigid structures such as crystals. Additionally, the insufficiency originates from the reversibility of quantum mechanics over time, compared to the finite life of all biological processes.
Particularly distressing for Santilli is the study of the DNA structure via the elementary mathematics of the 20th century, such as conventional numbers dating back to pre-biblical times, while the complexity of biological processes is simply beyond our imagination at this time.
1.11. INSUFFICIENCIES OF ASTROPHYSICS AND COSMOLOGY
According to Santilli, the climax of the scientific obscurantism of the 20th century can be seen in astrophysics and cosmology, because these disciplines have seen true extremes in the adaptation of the universe to verify Einsteinian doctrines without a serious scrutiny.
To begin, the study of the antimatter component of the universe, the consequential expected existence of antigravity between matter and antimatter and related topics, have been systematically ignored because notoriously not compatible with Einsteinian doctrines (Sections 2.4 and 3.7).
Additionally, Santilli has shown that the ongoing views on the expansion of the universe, the acceleration of the expansion with the distance, and the so-called "big bang" theory, are a consequence of the studious intent of preserving the constancy of the speed of light throughout the universe. On serious scientific grounds, we can say that the speed of light is indeed a constant under the conditions established by experiments until now, when propagating in vacuum conceived as a totally empty space.
However, Santilli insists that the claim of ``the universal constancy of the speed of
light" without the crucial words ``in vacuum" has a political, rather than a scientific character because disproved by
evidence when dealing with propagation of light within physical
media. It is today well established that the speed of electromagnetic waves C = c/n has the constant value c only in vacuum, while having otherwise a locally varying character depending on the characteristics of the medium in which it propagates represented by the index of refraction n. Santilli argues that at intergalactic distances, space cannot be considered empty, thus voiding the foundations of current cosmological theologies.
Additionally, Santilli gas shown (see Chapter 6) that: the ongoing theology on "dark matter" is a direct consequence of the studious intent of maintaining the constancy of the speed of light also within the physical medium inside a galaxy; the additional theology of "dark energy" is due to the additional studious assumption of maintaining the conventional speed of light in vacuum as equally valid in the interior of gravitational collapse and black holes; and that the assumption within physical media, particularly within the hyperdense media as in the interior of a black holes, of a maximal causal speed different than that in vacuum completely eliminates any need for the hyperbolic "dark matter" and "dark energy."
Above all, one of Santilli's major contribution in astrophysics and cosmology has been the focusing of the attention on ether as a fundamental universal medium (substratum) with very high energy density. A star at its initiation synthesizes from hydrogen a very large number of neutrons estimated to be of the order of 1050 neutrons per second or more. But the synthesis of a neutron requires 0.782 MeV, as noted above. According to orthodox views the missing energy is provided by the star environment. However, in this case a star could never initiate to produce light, since at its initiation the star would lose (rather than produce) energy at the rate of 1050 MeV per second or more.
The sole possibility for a scientific solution of this fundamental problem is the ether conceived as a universal substratum with very large energy density whose study is seen by Santilli as the ultimate frontier of knowledge, with possible advances simply beyond our most vivid imagination at this time, such as possible longitudinal communications through space at speeds millions of times bigger than that of the transversal electromagnetic waves, or travel to the stars at unrestricted speeds without fuel tanks (Santilli isogeomnetric propulsion, see Chapter 2) because the needed propulsion and energy may be available everywhere in the ether, provided, of course, we have basically new theories suitable for a serious study of these advances.
As we shall see, one of the ultimate motivations for the construction of hadronic mechanics has been to provide means for quantitative studies of possible interchanges between the ether as a universal substratum and the visible world, a study definitely not possible with quantum mechanics.
1.12. INTRODUCTORY READINGS
Scholars with a serious interest in acquiring an in-depth knowledge of Santilli's discoveries, are suggested to initiate their study with introductory readings, rather than with technical treatments, since the latter may appear to be disconnected from the larger scientific edifice. A first recommended reading is that on the insufficiencies of the 20th century theories available in the
A comprehensive technical presentation of said insufficiencies can be found in the monograph available for free download in pdf format
Hadronic Mathematics, Mechanics and Chemistry, Volume I: Limitations of Einstein's Special and General Relativities,
Quantum Mechanics and Quantum Chemistry
R. M. Santilli, International Academic Press (2008)
Santilli has been one of the firsts to present in 1981 various arguments according to which quarks cannot be physical particles in our spacetime. See the paper
An intriguing legacy of Einstein, Fermi, Jordan and others:
The possible invalidation of quark conjectures
R. M. Santilli,
Found. Phys. Vol. 11, 384-472 (1981).
A detailed technical treatment of the insufficiencies of 20th century theories and a denunciation of their lack of addressing dated 1984 was presented by Santilli in the book also available in free pdf download
Ethical Probe of Einstein's Followers in the USA: An Insider's View
R. M. Santilli, Alpha Publishing (1984)
The related 1,315 pages long documentation dated 1985 is also available in free pdf download from
Documentation of the Ethical Probe, Voplume I
Documentation of the Ethical Probe, Volume II
Documentation of the Ethical Probe, Volume III
R. M. Santilli, Alpha Publishing (1985)
The Foundation is attempting to secure copies of Santilli's personal documentation following 1985 that has been donated to a European Institution.
As an example of numerous available qualified doubts on the status of the 20th century science, it is also recommendable to read the following book by J. Dunning-Davies of the University of Hull, England and references quoted therein
"Exploding a Myth"
J. Dunning-Davies,Horwood Publishing, England (2007)
In this presentation, we follow Santilli in using the terms "Einstein's special relativity" as political parlance, since special relativity was initiated by Lorentz, received major contributions by Poincare' and was completed by Einstein without quotation of Poincare's contributions (despite existing correspondence prior to 1905), with additional contributions by Minkowski, Weyl and others. Therefore, in the event a paternity is requested, an appropriate scientific name should be the Lorentz-Poincare'-Einstein special relativity.
For a historical account outside manipulations of scientific history by organized academic interests, the Foundation suggests the reading of the book by A. A. Logunov. Director of the High Energy Physics Laboratory of Protvino, Russia
"Henri Poincare' and Relativity Theory"
A. A. Logunov, Moscow Nauka (2005)